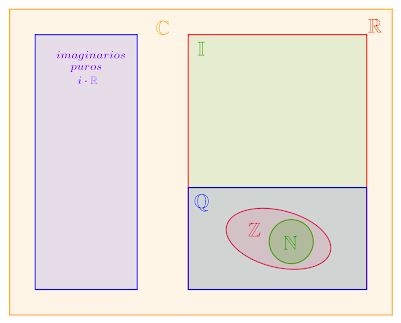
Los conjuntos de números los podemos poner en un esquema de este estilo:
$$ \Huge \mathbb{I} \bigcap \mathbb{Q} = \varnothing $$
Esto quiere decir que no existe ningún número real que sea racional e irracional a la vez; si es racional, se puede poner en forma de fracción luego no es irracional y viceversa.
$$ \Huge \mathbb{I} \bigcup \mathbb{Q} = \mathbb{R}$$
Esto quiere decir, que todo número real o es racional o es irracional.
$$ \Huge \left . \begin{array}{r} \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \cr \mathbb{I} \end{array}\right \} \subset \mathbb{R} \subset \mathbb{C} $$
Veamos ejemplos de números de distintos conjuntos:
$1, 13, 1.000.000, 5^2, ... \in \mathbb{N} $
$1, 13, 1.000.000, 5^2, 13, 0, -12, 3^0, -2.222.222, ... \in \mathbb{Z} $
$1, 13, 1.000.000, 5^2, 13, 0, -12, 3^0, -2.222.222, \dfrac{1}{2}, \dfrac{-11}{4}, \dfrac{23}{5} ... \in \mathbb{Q} $
$ \sqrt{2}, \sqrt{3}, \sqrt{p} \text{ siendo } p \text{ primo}, \log(2), \pi, e. \phi, ... \in \mathbb{I} $
Todos los números anteriores son números reales y por tanto son números complejo.
$i$ es la unidad imaginaria $i = \sqrt{-1}$ y tal que $i^2 = -1$ Veamos las potencias de $i$
$$\Large i^1 = i \qquad i^2 = -1 \qquad i^3 = -i \qquad i^4 = 1$$
$$\Large i^5 = i \qquad i^6 = -1 \qquad i^7 = -i \qquad i^8 = 1$$
$$\Large i^9 = i \qquad i^{10} = -1 \qquad i^{11} = -i \qquad i^{12} = 1$$ y así sucesivamente.
Para calcular cuanto vale cualquier potencia de $i, i^{75}$, lo que hacemos es la división entera del exponente entre 4 y nos quedaremos con el resto:
$$ \Large 75 = 4 \times 18 + 3 \Rightarrow i^{75} = i^{4 \times 18 + 3} = (i^4)^{18} \cdot i^3 = 1 \cdot i^3 = i^3 = -i$$
Veamos una definición formal del conjunto de los números complejos:
$$\Huge \mathbb{C} = \{ \ a + bi \ | \ a, b \in \mathbb{R}; \ \ i^2 = -1 \} $$
Sea un número complejo cualquiera $z = a + bi $, se define el conjugado $\bar{z} = a - bi$, es decir, la misma parte real y parte imaginaria la opuesta.
En esta animación de GeoGebra vamos a ver la representación del un número complejo $z$ (en la animación es el que forma el ángulo con la parte positiva del eje de abscisas $OX$), su conjugado $\bar{z}$, el opuesto $-z$ y el opuesto del conjugado $-\bar{z}$. Si cogemos el punto que determina dicho número complejo, el afijo, podemos mover dicho número y como se actualizan los 4 números según se desplaza.
Si un número complejo es $z = 3 + 5i$, su conjugado $\bar{z} = 3 - 5i$, su opuesto es $-z = -3 - 5i$; y el opuesto de su conjugado (es lo mismo el conjugado de su opuesto) es $- \bar{z} = - 3 + 5i$.
Otro ejemplo: $w = -6 - 7i$, su conjugado $\bar{w} = -6 + 7i$, su opuesto es $-w = 6 + 7i$ y el opuesto del conjugado $- \bar{w} = +6 - 7i$.
Distintas formas en las que podemos escribir un número complejo, siendo $r = | z | = \sqrt{a^2 + b^2}$ y $\alpha = Arg(z) = \arctg \left ( \dfrac{b}{a} \right )$.
$$ \large z = \left (a, b \right ) = a + bi = r \cdot \left ( \cos \alpha + i \sen \alpha \right ) = r_{\alpha} = r \cdot e^{i \alpha} $$
$$ \Large \textcolor{blue}{ \fbox{ $ \text{ Par ordenado } \qquad z = \left (a, b \right ) $ } } $$
$$ \Large \textcolor{blue}{ \fbox{ $ \text{Forma binómica } \qquad z = a + bi $ } } $$
$$ \Large \textcolor{blue}{ \fbox{ $ \text{Forma trigonométrica} \qquad z = r \cdot \left ( \cos \alpha + i \cdot \sen \alpha \right ) $ } } $$ $$ \Large \textcolor{blue}{ \fbox{ $ \text{Forma polar} \qquad z = r_{ \alpha } $ } } $$
$$ \Large \textcolor{blue}{ \fbox{ $ \text{Forma exponencial} \qquad z = r \cdot e^{ i \alpha } $ } } $$
Propiedades de los módulos de los números complejos:
- El $|z| \geq 0 $. Además $|z| = 0$ si y solo si $z = 0$.
- $|a| \leq |z|$ y $|b| \leq |z| $.
$|a|= \msqrt{a^2} \leq \msqrt{a^2 + b^2} = |z| $
$|b|= \msqrt{b^2} \leq \msqrt{a^2 + b^2} = |z| $
- El producto de un número complejo por su conjugado es igual al cuadrado de su módulo: $z \cdot \overline{z} = |z|^2$.
$$ z \cdot \overline{z} = (a + bi) \cdot (a - bi) = a^2 - (bi)^2 = a^2 + b^2 = |z|^2 $$
- El módulo de un número complejo y su conjugado son iguales: $|z| = |\overline{z}| $
Sea $z = a + bi$, el módulo de $|z| = \msqrt{a^2 + b^2}$
Sea $\overline{z} = a - bi$, el módulo de $|\overline{z}| = \msqrt{a^2 + (-b)^2} = \msqrt{a^2 + b^2} = |z| $
De la misma forma se puede ver que $$ |z| = |\overline{z}| = |-z| = |-\overline{z}| $$ - El módulo del producto de dos números complejos es el producto de sus módulos: $ |z_1 \cdot z_2 | = |z_1| \cdot |z_2|$
Vamos a utilizar las propiedades $ z \cdot \bar{z} = |z|^{2} $ y $\overline{z_1 \cdot z_2} = \bar{z_1} \cdot \bar{z_2} $ : $$ |z_1 \cdot z_2|^{2} = (z_1 \cdot z_2) \overline{ (z_1 \cdot z_2)} = z_1 \cdot z_2 \cdot \bar{z_1} \cdot \bar{z_2} = z_1 \cdot \bar{z_1} \cdot z_2 \cdot \bar{z_2}= |z_1|^{2}|z_2|^{2} $$ Sacamos raíces cuadradas tenemos: $$ |z_1 \cdot z_2| = |z_1| \cdot |z_2| $$ Nota: Está propiedad se puede extender al producto de 3, 4, 5, .... módulos de números complejos.
Consecuencia:
El módulo de la enésima potencia es la enésima potencia del módulo: $|z^n| = |z|^n$
- Sea un número complejo distinto de cero $z \neq 0$, el módulo del inverso es el inverso del módulo de $z$: $ \left | z^{-1} \right | = |z|^{-1} $
Usamos la propiedad anterior, $ |z_1 \cdot z_2 | = |z_1| \cdot |z_2|$
Tenemos que $$1 = z \cdot z^{-1} \Rightarrow 1 = |1| = \left| z \cdot z^{-1} \right | = |z| \cdot \left|z^{-1}\right| $$ Si despejamos $ \left|z^{-1}\right| $ tenemos que
$$ \left | z^{-1} \right| = \dfrac{\ \ 1 \ \ }{|z|} = |z|^{-1} $$
- El módulo del cociente de dos complejos es el cociente de sus módulos: $\text{ Si } z_2 \neq 0 \Rightarrow \left| \dfrac{\ z_1\ }{z_2} \right | = \dfrac{\ |z_1|\ }{ |z_2| } $
Usamos la dos propiedades anteriores: $ |z_1 \cdot z_2 | = |z_1| \cdot |z_2| $, $\left |z^{-1} \right | = |z|^{-1}$ y $|z_2| \neq 0$. Veamos: $$ \left | \dfrac{\ z_1\ }{z_2} \right | = \left |z_1 \cdot z_2^{-1} \right | = |z_1| \cdot \left|z_2^{-1} \right | = |z_1| \cdot |z_2|^{-1} = \dfrac{\ |z_1| \ }{|z_2|} $$
Fórmula de «De Moivre»
$$ \Large \textcolor{blue}{ \fbox{ $ \left( \cos \alpha + i \sen \alpha \right )^n = \cos n\alpha + i \sen n\alpha$ } } $$
$\bullet \quad $ Usando está fórmula podemos obtener las fórmulas trigonométricas del ángulo doble, $n = 2$:
Por un lado tenemos: $\left ( \cos \alpha + i \sen \alpha \right )^2 = \cos^2 \alpha + 2i\cos \alpha \sen \alpha - \sen^2 \alpha$
Por otro lado: $\cos 2\alpha + i \sen 2\alpha$
Como es el mismo número complejo, las partes real e imaginaria han de coincidir, entonces:
$$ \cos 2\alpha = \cos^2 \alpha - \sen^2 \alpha $$ $$ \sen 2 \alpha = 2\cos \alpha \sen \alpha $$
$\bullet \quad $ Veamos el caso $n = 3$, las fórmulas del ángulo triple:Por un lado tenemos: $\left ( \cos \alpha + i \sen \alpha \right )^3 = \cos^3 \alpha + 3i\cos^2 \alpha \sen \alpha + 3 \cos \alpha (i \cdot \sen \alpha)^2 + (i \cdot \sen \alpha )^3 = $ $$ = \cos^3 \alpha + 3i\cos^2 \alpha \sen \alpha - 3 \cos \alpha \sen^2 \alpha - i \sen^3 \alpha $$
Por otro lado: $\cos 3\alpha + i \sen 3\alpha$
Como es el mismo número complejo, las partes real e imaginaria han de coincidir, entonces:
$$ \cos 3 \alpha = \cos^3 \alpha - 3 \cos \alpha \sen^2 \alpha = \cos^3 \alpha - 3 \cos \alpha (1 - \cos^2 \alpha) = 4\cos^3 \alpha - 3 \cos \alpha $$ $$ \sen 3 \alpha = 3\cos^2 \alpha \sen \alpha - \sen^3 \alpha = 3(1 - \sen^2 \alpha ) \sen \alpha - \sen^3 \alpha = 3 \sen \alpha - 3 \sen^3 \alpha - \sen^3 \alpha = 3 \sen \alpha - 4 \sen^3 \alpha $$
Operaciones con números complejos
Las distintas expresiones utilizadas para representar un número complejo, nos deben hacer plantearnos cuál de ellas es la más adecuada para la realización de las distintas operaciones con números complejos.
| Cartesiana (a, b) |
Binómica a + bi |
Trigonométrica $r \cdot (\cos \alpha + i \cdot \sen \alpha ) $ |
Polar $r_{\alpha}$ |
Exponencial $r \cdot e^{i \cdot \alpha}$ |
|
|---|---|---|---|---|---|
| Suma | * | * | |||
| Resta | * | * | |||
| Producto | * | * | |||
| División | * | * | |||
| Potencia | * | * | * | ||
| Radicación | * |
Vamos con un ejemplo, calcular $(1 - i)^5$:
Para calcular $(1 - i)^5$ podemos usar el binomio de Newton:
$$ \displaystyle (1 - i)^5 = [1 + (- i) ]^5 = \sum_{n = 0}^{5} \binom{5}{n} 1^{5-n}(-i)^n = $$
$$ = \binom{5}{0} 1^{5} + \binom{5}{1} 1^{4}(-i)^1 + \binom{5}{2} 1^{3}(-i)^2 + \binom{5}{3} 1^{2}(-i)^3 + $$
$$ \displaystyle + \binom{5}{4} 1^{1}(-i)^4 + \binom{5}{5}(-i)^5 = 1 + 5(-i) + 10 (-1) + 10i + 5 - i = -4 + 4i $$
Pasamos el número de binómica a trigonométrica y polar $ z = 1 - i $:
$r = |z| = \sqrt{1^2 + (-1)^2} = \sqrt{2}$ y $\alpha = Arg( z ) = \arctg \left ( \dfrac{b}{a} \right ) = \arctg \left ( \dfrac{-1}{1} \right ) = \arctg( -1) $
Puede ser $\dfrac{3\pi}{4} = \gss{135}$ o $\dfrac{7\pi}{4} = \gss{315}$; es la $2^{\underline{a}}$ opción ya que $1 - i$ está en el $4^{\underline{o}}$ cuadrante.
$ = \sqrt{2}_{ \gss{315} } = \sqrt{2} \cdot \left [ \cos \left ( \gss{315} \right ) + i \sen \left ( \gss{315} \right ) \right ] $
Si calculamos su potencia:
$z^5 = (1 - i)^5 = \left ( \sqrt{2}_{ \dfrac{7\pi}{4} } \right )^5 = (\sqrt{2})^5_{ \dfrac{35\pi}{4} } = 4 \sqrt{2} \cdot \left [ \cos \left ( \dfrac{3\pi}{4} \right ) + i \sen \left ( \dfrac{3\pi}{4} \right ) \right ] = $
$= 4 \cdot \sqrt{2} \cdot \left [ \dfrac{ -\sqrt{2} }{2} + i \dfrac{ \sqrt{2} }{2} \right ] = - 4 + 4i $
Teorema: Sea $a(x)$ un polinomio con coeficientes reales, $a_i \in \R \ \forall i = 0, 1, 2, \ldots, n$: $$a(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots +a_{1} x+a_{0}$$ y sea $z \in \mathbb{C}$ es una raíz de $a(x)$, es decir $a(z) = 0 $, entonces $\bar{z}$ es también raíz de $a(x)$, es decir, $a(\bar{z}) = 0$.
Demo: Al ser $z$ raíz de $a(x)$ sabemos que $$ a(z) = a_{n} z^{n} + a_{n-1} z^{n-1} + \cdots + a_{1} z + a_{0} = 0 $$
Ahora bien, utilizando propiedades del conjugado de un número complejo y el hecho de que los coeficientes del polinomio son números reales, tenemos que:
$$\begin{aligned} a(\bar{z}) &=a_{n} \bar{z}^{n}+a_{n-1} \bar{z}^{n-1}+\cdots+a_{1} \bar{z}+ a_{0} = \\ & =\bar{a}_{n} \bar{z}^{n}+\bar{a}_{n-1} \bar{z}^{n-1}+\cdots+\bar{a}_{1} \bar{z}+a_{0} = \\ &=\overline{a_{n} z^{n}}+\overline{a_{n-1} z^{n-1}}+\dots+\overline{a_{1} z}+\overline{a_{0}} = \\ & =\overline{a_{n} z^{n}+a_{n-1} z^{n-1}+\cdots+a_{1}z+a_{0} } = \overline{0} = 0 \end{aligned}$$
Ejercicios con solución:
Para tener una expersión más manejable de dicho número, lo que tenemos que hacer es multiplicar numerador y denominador por el conjugado del denominador $(-2 - 3i)$:
$$\dfrac{4x + 9i}{-2 + 3i} = \dfrac{ (4x + 9i) \cdot (-2 - 3i) }{ (-2 + 3i) \cdot (-2 - 3i) } = \dfrac{-8x - 12ix - 18i + 27}{ 4 + 9 } = = \dfrac{-8x + 27 - 6i \cdot (2x + 3) }{ 13 }$$
Valor de $x$ para que sea un número real:
Para que sea un número real la parte imaginario tiene que ser cero. Veamos: $$ 2x + 3 = 0 \Rightarrow x = \mfrac{-3}{2} $$
Valor de $x$ para que sea un número imaginario puro.
Para que sea un número imaginario puro, la parte real ha de ser cero. Veamos: $$ -8x + 27 = 0 \Rightarrow \ x = \mfrac{27}{8} $$
Primero vamos a calcular su modulo:
$|z| = | (30 - 16 \cdot i) | \cdot | (a + 36 \cdot i) | $ si calculamos los módulos por separado:
$\sqrt{30^2 + 16^2} \cdot \sqrt{a^2 + 36^2} = 1.530 \ \Rightarrow \sqrt{1.156} \cdot \sqrt{a^2 + 1.296} = 1.530 \Rightarrow $
$ \Rightarrow 34 \cdot \sqrt{a^2 + 1.296} = 1.530 \Rightarrow \sqrt{a^2 + 1.296} = 45 \Rightarrow a^2 + 1.296 = 2.025 \Rightarrow a^2 = 729 \Rightarrow a = \pm 27$
Pero nos piden que valor de $a$ hace que el complejo $z$ esté en el primer cuadrante: $$ z = 30a + 576 + i \cdot (1.080 - 16a) $$ Si $a = +27 \ \Rightarrow \ z = 810 + 576 + i \cdot (1.080 + 432 ) = 1.386 + 648i $ que está en el $\odn{1}{er}$ cuadrante. $\checkmark$
Si $a = -27 \ \Rightarrow \ z = -810 + 576 + i \cdot (1.080 + 432 ) = -234 + 1.512i $ que no está en el $1^{\underline{er}}$ cuadrante. $\unicode{x2717}$
Sean $z = a + bi, \Rightarrow \overline{z} = a - bi$ los números complejos;
La suma es 8, entonces $$ z + \overline{z} = 8 \Rightarrow( a + bi ) + ( a - bi) = 8 \Rightarrow 2a = 8 \Rightarrow a = 4$$ La suma de los módulos es 10, entonces
$ | z | + | \overline{z} | = 10 \Rightarrow \sqrt{a^2 + b^2} + \sqrt{a^2 + b^2} = 10 \Rightarrow 2 \sqrt{16 + b^2} = 10 \Rightarrow \sqrt{16 + b^2} = 5 \Rightarrow $
$ \Rightarrow 16 + b^2 = 25 \Rightarrow b^2 = 9 \Rightarrow b = \pm 3 $
Luego los números son: $$z = 4 + 3i, \Rightarrow \overline{z} = 4 - 3i \text{ o } z = 4 - 3i, \Rightarrow \overline{z} = 4 + 3i $$
Tenemos que calcular las raíces sextas de -8i, $ z = \sqrt[6]{-8i} = \sqrt[6]{8_{ \frac{ 3\pi}{2} }}$. Para calcular las raíces sextas de un número tendremos que buscar $w$ tal que $w^6 = z$, para ello
$ |w| = \sqrt[6]{|z|} \Rightarrow |w| = \sqrt[6]{8} = \sqrt[6]{2^3} = \sqrt{2} $ y los argumentos:
$$ \beta = \dfrac{Arg(z) + 2 \pi k}{ n } = \dfrac{Arg(z) + \gss{360} k}{ n } , \text{ con } k = 0, 1, 2, ... , n - 1$$
En este caso el $Arg(-8i) = \dfrac{3\pi}{2} = \gss{270}$ y $\beta = \dfrac{ \dfrac{ 3\pi}{2} + 2 \pi k}{ 6 } = \dfrac{ \gss{270} + \gss{360} k}{ 6 }, k = 0, 1, 2, 3, 4 \text{ y } 5 $
$$k = 0 \text{ y} \beta_0 = \dfrac{ 3\pi }{ 12 } = \dfrac{ \pi }{ 4 } \Rightarrow \beta_0 = \gss{45} $$ $$k = 1 \text{ y} \beta_1 = \dfrac{ \dfrac{3\pi}{2} + 2 \pi}{ 6 } = \dfrac{ 7 \pi}{ 12 } \Rightarrow \beta_1 = \dfrac{ \gss{270} + \gss{360}}{ 6 } = \dfrac{ \gss{630} }{ 6 } = \gss{105} $$ $$k = 2 \text{ y} \beta_2 = \dfrac{ \dfrac{3\pi}{2} + 4 \pi}{ 6 } = \dfrac{ 11 \pi}{ 12 } \Rightarrow \beta_2 = \dfrac{ \gss{270} + \gss{360} \cdot 2}{ 6 } = \dfrac{ \gss{270} + \gss{720} }{ 6 } = \dfrac{ \gss{900} }{ 6 } = \gss{165} $$ $$k = 3 \text{ y} \beta_3 = \dfrac{ \dfrac{3\pi}{2} + 6 \pi}{ 6 } = \dfrac{ 15 \pi}{ 12 } \Rightarrow \beta_3 = \dfrac{ \gss{270} + \gss{360} \cdot 3 }{ 6 } = \dfrac{ \gss{270} + \gss{1.080} }{ 6 } = \dfrac{ \gss{1.260} }{ 6 } = \gss{225} $$ $$k = 4 \text{ y} \beta_4 = \dfrac{ \dfrac{3\pi}{2} + 8 \pi}{ 6 } = \dfrac{ 19 \pi}{ 12 } \Rightarrow \beta_4 = \dfrac{ \gss{270} + \gss{360} \cdot 4 }{ 6 } = \dfrac{ \gss{270} + \gss{1.440} }{ 6 } = \dfrac{ \gss{1.620} }{ 6 } = \gss{285} $$ $$k = 5 \text{ y} \beta_5 = \dfrac{ \dfrac{3\pi}{2} + 10 \pi}{ 6 } = \dfrac{ 23 \pi}{ 12 } \Rightarrow \beta_5 = \dfrac{ \gss{270} + \gss{360} \cdot 5 }{ 6 } = \dfrac{ \gss{270} + \gss{1.800} }{ 6 } = \dfrac{ \gss{2.070} }{ 6 } = \gss{345} $$ Es decir, las raíces son:
$w_0 = \sqrt{2}_{\frac{ \pi }{ 4 } } = \sqrt{2} \cdot \left [ \cos \left ( \dfrac{ \pi }{ 4 } \right ) + i \sen \left ( \dfrac{ \pi }{ 4 } \right ) \right ] = \sqrt{2} \cdot \left ( \dfrac{ \sqrt{2} }{2} + i \dfrac{ \sqrt{2} }{2} \right ) = 1 + i $
$w_1 = \sqrt{2}_{ \frac{ 7\pi }{ 12 } } = \sqrt{2} \cdot \left [ \cos \left ( \dfrac{ 7\pi }{ 12 } \right ) + i \sen \left ( \dfrac{ 7\pi }{ 12 } \right ) \right ] = \sqrt{2} \cdot \dfrac{ \sqrt{2} }{4} \cdot \left ( 1 - \sqrt{3} + i ( 1 + \sqrt{3} ) \right ) = $
$= \dfrac{ 1 - \sqrt{3} }{2} + i \dfrac{ 1 + \sqrt{3} }{2} $
$w_2 = \sqrt{2}_{ \frac{ 11 \pi}{ 12 } } = \sqrt{2} \cdot \left ( \cos \left ( \dfrac{ 11\pi }{ 12 } \right ) + i \sen \left ( \dfrac{ 11\pi }{ 12 } \right ) \right ) = \sqrt{2} \cdot \dfrac{ \sqrt{2} }{4} \cdot \left ( - (\sqrt{3} + 1) + i ( \sqrt{3} - 1) \right ) = $
$= - \dfrac{ \sqrt{3} + 1 }{2} + i \dfrac{ \sqrt{3} - 1 }{2} $
$w_3 = \sqrt{2}_{ \frac{ 15 \pi}{ 12 } } = \sqrt{2} \cdot \left [ \cos \left ( \dfrac{ 15\pi }{ 12 } \right ) + i \sen \left ( \dfrac{ 15\pi }{ 12 } \right ) \right ] = \sqrt{2} \cdot \left ( \dfrac{ -\sqrt{2} }{2} + i \dfrac{ -\sqrt{2} }{2} \right ) = - (1 + i) $
$w_4 = \sqrt{2}_{ \frac{ 19 \pi}{ 12 } } = \sqrt{2} \cdot \left [ \cos \left ( \dfrac{ 19\pi }{ 12 } \right ) + i \sen \left ( \dfrac{ 19\pi }{ 12 } \right ) \right ] = \sqrt{2} \cdot \dfrac{ \sqrt{2} }{4} \cdot \left ( 1 - \sqrt{3} + i ( 1 + \sqrt{3} ) \right ) = $
$ = \dfrac{ \sqrt{3} - 1 }{2} - i\dfrac{ \sqrt{3} + 1 }{2} $
$w_5 = \sqrt{2}_{ \frac{ 23 \pi}{ 12 } } = \sqrt{2} \cdot \left [ \cos \left ( \dfrac{ 23\pi }{ 12 } \right ) + i \sen \left ( \dfrac{ 23\pi }{ 12 } \right ) \right ] \sqrt{2} \cdot \dfrac{ \sqrt{2} }{4} \cdot \left ( 1 + \sqrt{3} + i ( 1 - \sqrt{3} ) \right ) = $
$= \dfrac{ 1 + \sqrt{3} }{2} + i \dfrac{ 1 - \sqrt{3} }{2} $
En grados, las raíces son:
$w_0 = \sqrt{2}_{ \gss{45} } = \sqrt{2} \cdot \left [ \cos \left ( \gss{45} \right ) + i \sen \left ( \gss{45} \right ) \right ] = \sqrt{2} \cdot \left ( \dfrac{ \sqrt{2} }{2} + i \dfrac{ \sqrt{2} }{2} \right ) = 1 + i $
$w_1 = \sqrt{2}_{ \gss{105} } = \sqrt{2} \cdot \left [ \cos \left ( \gss{105} \right ) + i \sen \left ( \gss{105} \right ) \right ] = \sqrt{2} \cdot \dfrac{ \sqrt{2} }{4} \cdot \left ( 1 - \sqrt{3} + i ( 1 + \sqrt{3} ) \right ) = $
$= \dfrac{ 1 - \sqrt{3} }{2} + i \dfrac{ 1 + \sqrt{3} }{2} $
$w_2 = \sqrt{2}_{ \gss{165} } = \sqrt{2} \cdot \left [ \cos \left ( \gss{165} \right ) + i \sen \left ( \gss{165} \right ) \right ] = \sqrt{2} \cdot \dfrac{ \sqrt{2} }{4} \cdot \left ( - (\sqrt{3} + 1) + i ( \sqrt{3} - 1) \right ) = $
$= - \dfrac{ \sqrt{3} + 1 }{2} + i \dfrac{ \sqrt{3} - 1 }{2} $
$w_3 = \sqrt{2}_{ \gss{225} } = \sqrt{2} \cdot \left [ \cos \left ( \gss{225} \right ) + i \sen \left ( \gss{225} \right ) \right ] = \sqrt{2} \cdot \left ( \dfrac{ -\sqrt{2} }{2} + i \dfrac{ -\sqrt{2} }{2} \right ) = - (1 + i) $
$w_4 = \sqrt{2}_{ \gss{285} } = \sqrt{2} \cdot \left [ \cos \left ( \gss{285} \right ) + i \sen \left ( \gss{285} \right ) \right ] = \sqrt{2} \cdot \dfrac{ \sqrt{2} }{4} \cdot \left ( 1 - \sqrt{3} + i ( 1 + \sqrt{3} ) \right ) = $
$ = \dfrac{ \sqrt{3} - 1 }{2} - i\dfrac{ \sqrt{3} + 1 }{2} $
$w_5 = \sqrt{2}_{ \gss{345} } = \sqrt{2} \cdot \left [ \cos \left ( \gss{345} \right ) + i \sen \left ( \gss{345} \right ) \right ] = \sqrt{2} \cdot \dfrac{ \sqrt{2} }{4} \cdot \left ( 1 + \sqrt{3} + i ( 1 - \sqrt{3} ) \right ) = $
$= \dfrac{ 1 + \sqrt{3} }{2} + i \dfrac{ 1 - \sqrt{3} }{2} $
Luego $$ S = \left \{ w_4, w_5 \right \} \Rightarrow S = \left \{ \dfrac{ \sqrt{3} - 1 }{2} - i\dfrac{ \sqrt{3} + 1 }{2}, \dfrac{ \sqrt{3} + 1 }{2} + i \dfrac{ 1 - \sqrt{3} }{2} \right \} $$
Tenemos que resolver $z = \sqrt[4]{-i} = \sqrt[4]{ 1_{ \frac{3\pi}{2} } } = \sqrt[4]{ 1_{ \gss{270} } } $
Claramente $|z| = 1 $ y el argumento de $z \text{ es } Arg(z) = \dfrac{3\pi}{2} = \gss{270} $. Y los argumentos de las raíces son $$\beta = \dfrac{ \dfrac{ 3\pi}{2} + 2 \pi k}{ 4 } = \dfrac{ \gss{270} + \gss{360} k}{ 4 }, k = 0, 1, 2 \text{ y } 3 $$ $$k = 0 \text{ y } \beta_0 = \dfrac{ 3\pi }{ 8 } \Rightarrow \beta_0 = \gss{67,5} $$ $$k = 1 \text{ y } \beta_1 = \dfrac{ \dfrac{3\pi}{2} + 2 \pi}{ 4 } = \dfrac{ 7 \pi}{ 8 } \Rightarrow \beta_1 = \dfrac{ \gss{270} + \gss{360}}{ 4 } = \dfrac{ \gss{630} }{ 4 } = \gss{157,5} $$ $$k = 2 \text{ y } \beta_2 = \dfrac{ \dfrac{3\pi}{2} + 4 \pi}{ 4 } = \dfrac{ 11 \pi}{ 8 } \Rightarrow \beta_2 = \dfrac{ \gss{270} + \gss{360} \cdot 2}{ 4 } = \dfrac{ \gss{270} + \gss{720} }{ 4 } = \dfrac{ \gss{990} }{ 4 } = \gss{247,5} $$ $$k = 3 \text{ y } \beta_3 = \dfrac{ \dfrac{3\pi}{2} + 6 \pi}{ 4 } = \dfrac{ 15 \pi}{ 8 } \Rightarrow \beta_3 = \dfrac{ \gss{270} + \gss{360} \cdot 3 }{ 4} = \dfrac{ \gss{270} + \gss{1.080} }{ 4 } = \dfrac{ \gss{1.350} }{ 4 } = \gss{337,5} $$ Tenemos que los ángulos $\gss{67,5}$ y $\gss{22,5}$ son complementarios. Y para calcular las razones trigonométricas $\gss{22,5}$ vamos a utilizar las fórmulas del ángulo mitad:
$$ \cos \left ( \dfrac{x}{2} \right ) = \pm \sqrt{ \dfrac{1 + cos( x ) }{2} }; \qquad \qquad \sen \left ( \dfrac{x}{2} \right ) = \pm \sqrt{ \dfrac{1 - cos( x ) }{2} }; $$ \\ Para calcular las razones trigonométricas de $\gss{67,5}$, usamos que es complementario de $\gss{22,5}$: \\ $\cos( \gss{67,5} ) = \sen( \gss{22,5} ) = \sen \left ( \dfrac{ \gss{45} }{2} \right ) = \sqrt{ \dfrac{1 - \cos( \gss{45} ) }{2} } = \sqrt{ \dfrac{1 - \dfrac{ \sqrt{2} }{2} }{2} } = \sqrt{ \dfrac{2 - \sqrt{2} }{4} } = $ \\ \\ $ = \dfrac{ \sqrt{ 2 - \sqrt{2} } }{2} $
$\sen( \gss{67,5} ) = \cos( \gss{22,5} ) = \cos \left ( \dfrac{\gss{45}}{2} \right ) = \sqrt{ \dfrac{1 + \cos( \gss{45} ) }{2} } = \sqrt{ \dfrac{1 + \dfrac{ \sqrt{2} }{2} }{2} } = \sqrt{ \dfrac{2 + \sqrt{2} }{4} } = $
$ = \dfrac{ \sqrt{ 2 + \sqrt{2} } }{2} $
En grados, las raíces son: $$w_0 = 1_{ \gss{67,5} } = \cos \left ( \gss{67,5} \right ) + i \sen \left ( \gss{67,5} \right ) = \dfrac{ \sqrt{2 - \sqrt{2}} }{2} + i \dfrac{ \sqrt{ 2 + \sqrt{2} } }{2} $$ $$w_1 = 1_{ \gss{157,5} } = \cos \left ( \gss{157,5} \right ) + i \sen \left ( \gss{157,5} \right ) = \dfrac{ - \sqrt{2 + \sqrt{2}} }{2} + i\dfrac{ \sqrt{ 2 - \sqrt{2} } }{2} $$ $$w_2 = 1_{ \gss{247,5} } = \cos \left ( \gss{247,5} \right ) + i \sen \left ( \gss{247,5} \right ) = \dfrac{ - \sqrt{2 - \sqrt{2}} }{2} - i\dfrac{ \sqrt{ 2 + \sqrt{2} } }{2} $$ $$w_3 = 1_{ \gss{337,5} } = \cos \left ( \gss{337,5} \right ) + i \sen \left ( \gss{337,5} \right ) = \dfrac{ \sqrt{2 + \sqrt{2}} }{2} - i \dfrac{ \sqrt{ 2 - \sqrt{2} } }{2} $$
Como es una potencia vamos a pasar el número a polares:
$3 + 3i \Rightarrow | 3 + 3i | = \sqrt{(3)^2 + (3)^2 } = \sqrt{18} = 3\sqrt{2}$ y $Arg(z) = \arctg \left ( \dfrac{\ 3 \ }{ 3 } \right ) = \arctg(1) = \dfrac{ \ \pi \ }{4} = \gss{45}$ $$ 3 + 3i = 3\sqrt{2}_{\frac{ \pi } {4} } = 3\sqrt{2}_{ \gss{45} }$$
Ahora calculamos la potencia:
$\left ( 3 + 3 \cdot i \right )^{829} = \left ( 3\sqrt{2}_{ \frac{ \pi } {4} } \right )^{829} = {3^{829} 2^{424} \sqrt{2} }_{ \frac{ 829\pi }{4} } = (*) $
Aquí el problema lo tenemos en calcular $\mfrac{ 829\pi }{4} $
$$ \dfrac{ 829\pi }{4} = 407\pi + \dfrac{ \pi }{4} = 406\pi + \pi + \mfrac{ \pi }{4} = \dfrac{ 5\pi }{4} (406\pi \text{ son 203 vueltas completas.} )$$
$= (*) = {3^{829}2^{424} \sqrt{2} }_{ \frac{ 5\pi }{4} } = 3^{829}2^{424} \sqrt{2} \cdot \left [ \cos \left ( \dfrac{ 5\pi }{4} \right ) + i \sen \left ( \dfrac{ 5\pi }{4} \right ) \right ] = 3^{829}2^{424} \sqrt{2} \cdot \left ( \dfrac{ -\sqrt{2} }{2} - i \dfrac{ \sqrt{2} }{2} \right ) = $
$ = - 3^{829}2^{424} \cdot ( 1 + i ) $
Lo primero que hay que hacer es calcular $i^{15} = i^{4.3 + 3} = i^3 = -i$. Luego despejar $z$
$$ \dfrac{z}{1 + z} = -i \Rightarrow z = -i \cdot (1 + z) \Rightarrow z = -i -iz \Rightarrow z ( 1 + i ) = -i \Rightarrow z = \dfrac{\ -i \ }{1 + i} = \dfrac{\ -i \cdot (1 - i) \ }{ (1 + i) \cdot (1 - i)} = \dfrac{\ -1 - i \ }{ 2 } $$
Como es un polinomio con coeficientes reales, vamos a probar con los divisores del término independiente, en este caso $-2$ y nos quedan $\pm 1 y \pm 2$.
Sea $p(z) = z^4 + z^3 - z^2 + z - 2 = 0$ si hacemos $p(1) = 1^4 + 1^3 - 1^2 + 1 - 2 = 3 - 3 = 0$ luego 1 es solución de la ecuación. Aplicamos Ruffini y nos queda:
$$p(z) = (z - 1) \cdot (z + 2) \cdot (z + i) \cdot (z - i) $$
Sacamos factor común $-x \cdot (x^4 + 1) = 0$ y seguir factorizando: $$-x \cdot (x^2 + i) \cdot (x^2 - i) = -x \cdot (x + i\sqrt{i} ) \cdot (x - i\sqrt{i} ) \cdot (x - \sqrt{i} ) \cdot (x + \sqrt{i} ) = 0$$ Otra forma de hacerlo, por ejemplo, si nos pidieran la forma binomial:
$x^4 = -1$ es decir, calcular las raíces 4 de -1, $x = \sqrt[4]{-1} = \sqrt[4]{1_{\gss{180}} } $
El módulo de la raíz $w, |w| = 1$. Así los argumentos de las raíces son:
$$\beta = \dfrac{ \pi + 2 \pi k}{ 4 } = \dfrac{ \gss{180} + \gss{360} k}{ 4 }, k = 0, 1, 2 \text{ y } 3 $$ $$k = 0 \text{ y } beta_0 = \dfrac{ \ \pi \ }{4} \Rightarrow \beta_0 = \gss{45} $$ $$k = 1\text{ y }\beta_1 = \dfrac{ \pi + 2 \pi}{ 4 } = \dfrac{ \ 3\pi \ }{ 4 } \Rightarrow \beta_1 = \dfrac{ \gss{180} + \gss{360} }{ 4 } = \gss{135} $$ $$k = 2\text{ y }\beta_2 = \dfrac{ \pi + 4 \pi}{ 4 } = \dfrac{ \ 5\pi \ }{ 4 } \Rightarrow \beta_2 = \dfrac{ \gss{180} + \gss{360} \cdot 2}{ 4 } = \dfrac{ \gss{900} }{ 4 } = \gss{225} $$ $$k = 3\text{ y }\beta_3 = \dfrac{ \pi + 6 \pi}{ 4 } = \dfrac{\ 7\pi \ }{ 4 } \Rightarrow \beta_3 = \dfrac{ \gss{180} + \gss{360} \cdot 3 }{ 4 } = \dfrac{ \gss{1.260} }{ 4 } = \gss{315} $$ Es decir, las raíces son:
$$w_0 = 1_{\frac{ \pi }{ 4 } } = \cos \left ( \dfrac{ \pi }{ 4 } \right ) + i \sen \left ( \dfrac{ \pi }{ 4 } \right ) = \dfrac{ \sqrt{2} }{2} + i \dfrac{ \sqrt{2} }{2} $$ $$w_1 = 1_{ \frac{ 3\pi }{ 4 } } = \cos \left ( \dfrac{ 3\pi }{ 4 } \right ) + i \sen \left ( \dfrac{ 3\pi }{ 4 } \right ) = - \dfrac{ \sqrt{2} }{2} + i \dfrac{ \sqrt{2} }{2} $$ $$w_2 = 1_{ \frac{ 5 \pi}{ 4 } } = \cos \left ( \dfrac{ 5\pi }{ 4 } \right ) + i \sen \left ( \dfrac{ 5\pi }{ 4 } \right ) = - \dfrac{ \sqrt{2} }{2} - i\dfrac{ \sqrt{2} }{2} $$ $$w_3 = 1_{ \frac{ 7 \pi}{ 4 } } = \cos \left ( \dfrac{ 7\pi }{ 4 } \right ) + i \sen \left ( \dfrac{ 7\pi }{ 4 } \right ) = \dfrac{ \sqrt{2} }{2} - i \dfrac{ \sqrt{2} }{2} $$ En grados, las raíces son:
$$w_0 = 1_{ \gss{45} } = \cos \left ( \gss{45} \right ) + i \sen \left ( \gss{45} \right ) = \dfrac{ \sqrt{2} }{2} + i \dfrac{ \sqrt{2} }{2} $$ $$w_1 = 1_{ \gss{135} } = \cos \left ( \gss{135} \right ) + i \sen \left ( \gss{135} \right ) = - \dfrac{ \sqrt{2} }{2} + i \dfrac{ \sqrt{2} }{2} $$ $$w_2 = 1_{ \gss{225} } = \cos \left ( \gss{225} \right ) + i \sen \left ( \gss{225} \right ) = - \dfrac{ \sqrt{2} }{2} - i \dfrac{ \sqrt{2} }{2} $$ $$w_3 = 1_{ \gss{315} } = \cos \left ( \gss{315} \right ) + i \sen \left ( \gss{315} \right ) = \dfrac{ \sqrt{2} }{2} - i \dfrac{ \sqrt{2} }{2} $$
No hay comentarios:
Publicar un comentario