Fracciones Parciales
Dos polinomios son iguales si tienen el mismo grado y sus coeficientes son iguales.
Si dos polinomios son iguales, coincide su valor para cualquier valor de $x$.
Fracciones Propias e Impropias
Definición: Se dice que una fracción racional $\dfrac{P(x)}{Q(x)}$ es una fracción propia, si el grado del polinomio $P(x)$ es menor que el grado del polinomio $Q(x)$. En caso contrario, es decir, si el grado de $P(x)$ es mayor o igual al de $Q(x)$, la fracción se llama impropia.
Toda fracción impropia se puede expresar, efectuando la división, como la suma de un polinomio mas una fracción propia. Es decir,
$$ \dfrac{P(x)}{Q(x)} = C(x) + \dfrac{d(x)}{Q(x)} $$
Vamos a descomponer un fracción propia en suma de fracciones más sencillas. Tenemos 4 casos:
Caso I: El denominador $Q(x)$ es un producto de factores lineales distintos. Esto significa que podemos escribir
$$ Q(x) = \left(a_{1} x + b_{1} \right) \left( a_{2} x + b_{2} \right ) \cdots \left( a_{k} x + b_{k} \right ) $$
en donde no hay factor que se repita. En este caso, existen constantes $A_{1}, A_{2}, \cdots, A_{k}$ tales que
$$ \dfrac{P(x)}{Q(x)} = \dfrac{A_{1}}{a_{1}x + b_{1}} + \dfrac{A_{2}}{a_{2} x + b_{2}} + \cdots + \dfrac{A_{k}}{a_{k} x + b_{k}} $$
Ejemplo 1: Descomponer en fracciones parciales la fracción: $$ \dfrac{7x + 3}{ x^2 + 3x - 4} $$
Tenemos que el denominador se puede descomponer en factores simples como sigue:
$$ x^2 + 3x - 4 = (x + 4)(x - 1) $$
Luego la descomposición en fracciones parciales es:
$$ \dfrac{7x + 3}{x^2 + 3x - 4} = \dfrac{7x + 3}{(x + 4)(x - 1)} = \dfrac{A}{x + 4} + \dfrac{B}{x - 1 } $$
Para encontrar los valores de $A$ y $B$, ponemos común denominador, obteniendo
$$ 7x + 3 = A(x - 1) + B(x + 4) $$
En este punto tenemos dos opciones:
a) Desarrollando e igualando las potencias de $x$ y el término independiente se obtiene el siguiente sistema de ecuaciones:
$$7x + 3 = Ax - A + Bx + 4B $$
De $x$ tenemos que $7x = Ax + Bx$;
del término independiente $ 3 = - A + 4B $
b) Calculando valores de los polinomios. ¿Qué valores de $x$ vamos a coger? Está claro, ¿no? Cogeremos las raíces, $x = 1$ y $x = -4$
Por lo que la fracción original queda:
$$ \dfrac{7x + 3}{x^2 + 3x - 4} = \dfrac{5}{x + 4} + \dfrac{2}{x - 1} $$
Ejemplo 2 $$ \dfrac{x^2 + 2x - 1}{2x^3 + 3x^2 - 2x } $$
Solución Se tiene que el denominador se puede factorizar como sigue:
$$ 2 x^3 + 3x^2 - 2x = x \left( 2x^2 + 3x - 2 \right ) = x(2x - 1)(x + 2) $$
Luego, la descomposición en fracciones parciales es:
$$ \dfrac{x^2 + 2x - 1}{x(2x - 1)(x + 2)} = \dfrac{A}{x} + \dfrac{B}{2x - 1} + \dfrac{C}{x + 2} $$
Ponemos denominador común y tenemos:
$$ \dfrac{x^2 + 2x - 1}{x(2x - 1)(x + 2)} = \dfrac{A(2x - 1)(x + 2) + Bx(x + 2) + Cx(2x - 1) }{x(2x - 1)(x + 2)} $$
igualando numeradores se obtiene
$$ x^2 + 2x - 1 = A(2x - 1)(x + 2) + Bx(x + 2) + Cx(2x - 1) \qquad (1) $$
En este punto tenemos dos opciones:
a) Desarrollando e igualando las potencias de $x$ y el término independiente se obtiene el siguiente sistema de ecuaciones: \\
$$ x^2 + 2x - 1 = A(2x^2 + 4x - x - 2) + B(x^2 + 2x) + C(2x^2 - x) $$
$$ x^2 + 2x - 1 = 2Ax^2 + 3Ax - 2A + Bx^2 + 2Bx + 2Cx^2 - Cx $$
$$ x^2 + 2x - 1 = x^2(2A + B + 2C) + x(3A + 2B - C) - 2A $$
es decir
$$A = \dfrac{1}{2}, \quad B = \dfrac{1}{5}, \quad \text{y} \quad C = -\dfrac{1}{10}$$
así
$$ \dfrac{x^2 + 2x - 1}{2x^3 + 3x^2 - 2x} = \dfrac{ \dfrac{1}{2} }{x} + \dfrac{ \dfrac{1}{5} }{2x - 1} + \dfrac{ - \dfrac{1}{10}}{x + 2} = \dfrac{ 1 }{2x} + \dfrac{ 1 }{5(2x - 1)} - \dfrac{ 1 }{10(x + 2)} $$
b) Calculando valores de los polinomios. Si en (1) damos valores tenemos:
$$ x^2 + 2x - 1 = A(2x - 1)(x + 2) + Bx(x + 2) + Cx(2x - 1) $$
$$x = 0 \Longrightarrow -1 = -2A \Rightarrow A = \dfrac{1}{2} $$
$$x = -2 \Longrightarrow -1 = C(-2)(2\cdot(-2) - 1) \Rightarrow -1 = 10C \Rightarrow C = -\dfrac{1}{10} $$
$$x = \dfrac{1}{2} \Longrightarrow \dfrac{1}{4} = B\dfrac{1}{2} \cdot \left ( \dfrac{1}{2} + 2 \right ) \Rightarrow \dfrac{1}{4} = B\dfrac{5}{4} \Rightarrow B = \dfrac{1}{5} $$
Caso II: El denominador $Q(x)$ es un producto de factores lineales, algunos de los cuales se repiten.
Si $Q(x)$ tiene un factor lineal repetido $k$ veces de la forma $\left(a_{1} x + b_{1}\right)^{k},$ entonces la descomposición en fracciones parciales contiene $k$ términos de la forma:
$$ \dfrac{A_{1}}{a_{1}x + b_{1}} + \dfrac{A_{2}}{\left(a_{1}x + b_{1} \right)^{2}} + \cdots + \dfrac{A_{k}}{\left(a_{1} x+b_{1}\right)^{k}} \text{ donde } A_{1}, A_{2}, \cdots, A_{k} \text{ son constantes. } $$ \\
Ejemplo 3 Descomponer en fracciones parciales:
$$ \dfrac{5x^2 - 36x + 48}{x(x - 4)^2} $$
La descomposicion en fracciones parciales es:
$$ \dfrac{5x^{2} -36x + 48}{x(x - 4)^{2}} = \dfrac{A}{x} + \dfrac{B}{(x - 4)} + \dfrac{C}{(x - 4)^{2}} $$
Poniendo denominador común
$$ \dfrac{5x^{2} -36x + 48}{x(x - 4)^{2}} = \dfrac{A(x - 4)^2 + Bx(x - 4) + Cx}{x(x - 4)^{2}} $$
Igualando numeradores tenemos
$$ 5x^2 - 36x + 48 = A(x - 4)^2 + Bx(x - 4) + Cx \qquad (2) $$
En este punto tenemos dos opciones:
a) Desarrollando e igualando las potencias de $x$ y el término independiente se obtiene el siguiente sistema de ecuaciones:
$$ 5x^2 - 36x + 48 = A(x^2 - 8x + 16) + B(x^2 - 4x) + Cx $$
$$ 5x^2 - 36x + 48 = x^2(A + B) + x(- 8A - 4B + C) + 16A $$
obteniendo el sistema:
Luego:
$$ \dfrac{5x^2 - 36x + 48}{x(x - 4)^2} = \dfrac{3}{x} + \dfrac{2}{x - 4} - \dfrac{4}{(x - 4)^2} $$
b) Calculando valores de los polinomios. Si damos valores en (2) tenemos: \\ \\
$x = 0 \Longrightarrow 48 = 16 A \Rightarrow A = \dfrac{48}{16} = 3 $ \\ \\
$x = 4 \Longrightarrow -16 = 4 C \Rightarrow C = \dfrac{-16}{4} = -4 $ \\ \\
$x = 1 \Longrightarrow 17 = 9A - 3B + C \Rightarrow 17 = 27 -3B -4 \Rightarrow -6 = -3B \Rightarrow B = 2 $
Ejemplo 4 Descomponer en fracciones parciales:
$$ \dfrac{4x - 4}{x^3 - 4x^2 + 4x} $$
Factorizamos el denominador
$$ x^3 - 4x^2 + 4x = x ( x - 2 )^2 $$
Por lo tanto, su descomposición en fracciones parciales es:
$$ \dfrac{4x - 4}{x ( x - 2 )^2} = \dfrac{A}{x} + \dfrac{B}{x - 2} + \dfrac{C}{(x - 2)^2} $$
poniendo común denominador:
$$ \dfrac{4x - 4}{x ( x - 2 )^2} = \dfrac{A( x - 2 )^2 + B x ( x - 2 ) + Cx}{x(x - 2)^2} $$
igualando numeradores tenemos:
$$ 4x - 4 = A( x - 2 )^2 + B x ( x - 2 ) + Cx \qquad \text{(4)}$$
En este punto tenemos dos opciones:
a) Desarrollando e igualando las potencias de $x$ y el término independiente se obtiene el siguiente sistema de ecuaciones:
$$ 4x - 4 = A( x - 2 )^2 + B x ( x - 2 ) + Cx $$
$$ 4x - 4 = Ax^2 -4Ax + 4A + Bx^2 - 2Bx + Cx $$
obteniendo el sistema:
Luego:
$$ \dfrac{4x - 4}{x^3 - 4x^2 + 4x} = \dfrac{-1}{x} + \dfrac{1}{x - 2} - \dfrac{2}{(x - 2)^2} $$
b) Calculando valores de los polinomios. Si damos valores en (4) tenemos:
$x = 2 \Longrightarrow 4 = 2C \Rightarrow C = \dfrac{4}{2} = 2 $
$x = 0 \Longrightarrow -4 = 4 A \Rightarrow A = \dfrac{-4}{4} = -1 $
$x = 1 \Longrightarrow 0 = A - B + C \Rightarrow B = A + C = 2 - 1 = 1 $
$$ \dfrac{x^4 - 2x^2 + 4x + 1}{x^3 - x^2 - x + 1 } $$
Comenzaremos por dividir los polinomios
$$ \dfrac{x^4 - 2x^2 + 4x + 1}{x^3 - x^2 - x + 1} = x + 1 + \dfrac{4x}{x^3 - x^2 - x + 1} $$
luego, factorizando el denominador $ x^3 - x^2 - x + 1 $ resulta
$$ x^3 - x^2 - x + 1 = (x + 1)(x - 1)^{2} $$
Por lo tanto, su descomposición en fracciones parciales es:
$$ \dfrac{4x}{(x+1)(x - 1)^2} = \dfrac{A}{x - 1} + \dfrac{B}{(x - 1)^2} + \dfrac{C}{x + 1} $$
poniendo denominador común:
$$ 4x = A(x + 1)(x - 1) + B(x + 1) + C(x - 1)^2 \qquad (5) $$
$$ 4x = A(x^2 - 1) + B(x + 1) + C(x^2 - 2x + 1) $$
$$ 4x = x^2(A + C) + x(B - 2C) - A + B + C $$
En este punto tenemos dos opciones:
a) Desarrollando e igualando las potencias de $x$ y el término independiente se obtiene el siguiente sistema de ecuaciones:
del cual de obtiene: $A = 1, \quad B = 2$ y $C = -1$ de modo que
$$ \dfrac{x^4 - 2x^2 + 4x + 1}{x^3 - x^2 - x + 1} = x + 1 + \dfrac{1}{x - 1} + \dfrac{2}{ (x - 1)^2 } - \dfrac{1}{x + 1} $$
b) Si damos valores en (5) tenemos:
$$x = 1 \Longrightarrow 4 = 2 B \Rightarrow B = 2 $$
$$x = -1 \Longrightarrow -4 = 4 C \Rightarrow C = -1 $$
$$x = 0 \Longrightarrow 0 = -A + B + C \Rightarrow 0 = -A + 2 - 1 \Rightarrow A = 1 $$
Al principio habéis visto que habría 4 casos, los dos que quedan los añadiré más adelante.
Lo primero que tenmos que haces es factorizar el denominador: $ x^2 - 5x + 6 $. Podemos usar la fórmula para resolver ecuaciones de segundo grado o Ruffini. Sea el método que sea, vemos que podemos factorizar el denominador $ x^2 - 5x + 6 = (x- 2) \cdot (x - 3)$
Así sabemos que $ \dfrac{5x + 13}{x^2 - 5x + 6} = \dfrac{A}{x - 2} + \dfrac{B}{x - 3} $ con $A$ y $B$ constantes.
$$ \dfrac{5x + 13}{x^2 - 5x + 6} = \dfrac{A}{x - 2} + \dfrac{B}{x - 3} = \dfrac{A \cdot (x -3) + B \cdot (x - 2) }{ (x - 2) \cdot (x - 3) } $$ Ahora tenemos que ver que $5x + 13 = A \cdot (x - 3) + B \cdot (x - 2) $ y para resolver esto, es decir, que dos polinomios son iguales lo podemos hacer de dos formas:
- Igualando coeficientes
- Evaluando valores
Vamos hacerlo evaluando valores:
Si $x = 2 \Rightarrow 5 \cdot 2 + 13 = - B \Rightarrow 23 = - B \Rightarrow B = -23 $
Si $x = 3 \Rightarrow 5 \cdot 3 + 13 = A \Rightarrow A = 28 $
Luego $$ \dfrac{5x + 13}{x^2 - 5x + 6} = \dfrac{28}{x - 3 } - \dfrac{23}{x - 2} $$
Lo primero que tenmos que haces es factorizar el denominador: $ x^3 + 6x^2 + 11x + 6 $. Usaremos Ruffini para calcuar las posibles raíces, vemos que las raíces no pueden ser positivas ya que nunca sería cero. Probamos con -1 y vemos que es raíz. Así tenemos que $x^3 + 6x^2 + 11x + 6 = (x + 1) \cdot (x^2 + 5x + 6)$ Si seguimos aplicando Ruffini tenemos que $x^3 + 6x^2 + 11x + 6 = (x + 1) \cdot (x + 2) \cdot (x + 3) $.
Así sabemos que $ \dfrac{6x^2 + 22x + 18}{x^3 + 6x^2 + 11x + 6} = \dfrac{A}{x + 1} + \dfrac{B}{x + 2} + \dfrac{C}{x +3} $ con $A$, $B$ y $C$ constantes.
$$ \dfrac{6x^2 + 22x + 18}{x^3 + 6x^2 + 11x + 6} = \dfrac{A}{x + 1} + \dfrac{B}{x + 2} + \dfrac{C}{x +3} = \dfrac{A \cdot (x + 2) \cdot (x + 3) + B \cdot (x + 1) \cdot (x + 3) + C \cdot (x + 1) \cdot (x + 2) } { (x + 1) \cdot (x + 2) \cdot (x + 3) } $$ Ahora tenemos que ver que $6x^2 + 22x + 18 = A \cdot (x + 2) \cdot (x + 3) + B \cdot (x + 1) \cdot (x + 3) + C \cdot (x + 1) \cdot (x + 2) $ y para resolver esto, es decir, que dos polinomios son iguales lo podemos hacer de dos formas:
- Igualando coeficientes
- Evaluando valores
Vamos hacerlo evaluando valores:
Si $x = -1 \Rightarrow 6 \cdot (-1)^2 + 22 \cdot (-1) + 18 = A \cdot (-1 + 2) \cdot (-1 + 3) \Rightarrow 2 = 2 \cdot A \Rightarrow A = 1 $
Si $x = -2 \Rightarrow 6 \cdot (-2)^2 + 22 \cdot (-2) + 18 = B \cdot (-2 + 1) \cdot (-2 + 3) \Rightarrow -2 = - B \Rightarrow B = 2 $
Si $x = -3 \Rightarrow 6 \cdot (-3)^2 + 22 \cdot (-3) + 18 = C \cdot (-3 + 1) \cdot (-3 + 2) \Rightarrow 6 = 2C \Rightarrow C = 3 $
Luego $$ \dfrac{6x^2 + 22x + 18}{x^3 + 6x^2 + 11x + 6} = \dfrac{1}{x + 1} + \dfrac{2}{x + 2} + \dfrac{3}{x + 3} $$
En este caso el grado de los polinomios del numerador y denominador son iguales, tenemos que hacer la división «en caja» y nos quedará:
$$ - (x^2 + 4x + 6) = (x^2 - 3x + 2) \cdot (-1) - ( 7x + 4 ) \Rightarrow - \dfrac{x^2 + 4x + 6 }{x^2 - 3x + 2} = - 1 - \dfrac{7x + 4}{x^2 -3x + 2} $$ Luego tenemos que descomponer $\dfrac{7x + 4}{x^2 -3x + 2}$ es fracciones simples:
El denominador $ x^2 - 3x + 2 $, como 1 es raíz se factoriza rápidamente $ x^2 - 3x + 2 = (x - 1) \cdot (x - 2) $ luego
$\dfrac{7x + 4}{x^2 -3x + 2} = \dfrac{A}{x - 1} + \dfrac{B}{x - 2} = \dfrac{ A \cdot (x - 2) + B \cdot (x - 1) }{ x^2 -3x + 2 }$
Evaluando tenemos:
Si $x = 1 \Rightarrow 7\cdot 1 + 4 = -A \Rightarrow A = -11 $
Si $x = 2 \Rightarrow 7\cdot 2 + 4 = B \Rightarrow B = 18 $
Luego $$ \dfrac{7x + 4}{x^2 -3x + 2} = \dfrac{-11}{x - 1} + \dfrac{18}{x - 2} $$ y por tanto $$ - \dfrac{x^2 + 4x + 6 }{x^2 - 3x + 2} = -1 - \dfrac{7x + 4}{x^2 - 3x + 2} = - 1 - \dfrac{18}{x - 2} + \dfrac{11}{x - 1} $$
$$ \dfrac{2}{x - 2} + \dfrac{1}{x - 1} + \dfrac{1}{(x - 1)^2} $$
$$ \dfrac{2}{(x - 2)^2} - \dfrac{2}{x + 3} - \dfrac{2}{x - 1} $$
$$ 1 + \dfrac{-3x^{2} + 14x + 32}{x^{3} + 2x^{2} - 4x - 8} = 1 + \dfrac{3}{x - 2} - \dfrac{6}{x + 2} + \dfrac{2}{(x + 2)^2} $$
Caso III: El denominador $Q(x)$ contiene factores cuadráticos irreductibles, ninguno de los cuales se repite.
Si $Q(x)$ tiene un factor cuadrático no repetido de la forma $ax^2 + bx + c$, en donde, $b^2 - 4ac < 0$, entonces la descomposición en fracciones parciales contiene un término de la forma:
$$ \dfrac{ Ax + B }{ ax^2 + bx + c } \qquad \text{ donde } A \text{ y } B \text{ son constantes } $$
Ejemplo 6 Descomponer en fracciones parciales: $$ \dfrac{4x^2 - 8x + 1}{x^3 - x + 6} $$ Tenemos que $$ \dfrac{ 4x^2 - 8x + 1 }{ x^3 - x + 6 } = \dfrac{4x^2 - 8x + 1}{(x + 2) \left( x^2 - 2x + 3 \right ) } = \dfrac{A}{x + 2} + \dfrac{B x + C}{x^2 - 2x + 3} $$ multiplicando por el común denominador: $$ 4x^2 - 8x + 1 = A \left( x^2 - 2x + 3 \right) + (Bx + C)(x + 2) \qquad (4) $$ $$ 4x^2 - 8x + 1 = Ax^2 - 2Ax + 3A + Bx^2 + 2Bx + Cx + 2C $$ $$ 4x^2 - 8x + 1 = x^2(A + B) + x(-2A + 2B + 2C) + 3A + 2C $$ obteniendo el sistema $$\left \{ \begin{array}{ll} A + B & = 4 \Rightarrow B = 4 - A \cr -2A + 2B + C & = -8 \\ %\quad \text { de donde } \quad A=3, B=1, C=-4 \cr 3A + 2C & = 1 \Rightarrow C = \dfrac{1 - 3A}{2} \end{array} \right. $$ Por lo tanto, $$ -2A + 2(4 - A) + \dfrac{1 - 3A}{2} = -8 \Rightarrow -4A + 16 - 4A + 1 - 3A = -16 \Rightarrow -11A = -33 \Rightarrow A = 3 $$ Luego $B = 4 - 3 = 1$ y $C = \dfrac{1 - 9}{2} = \dfrac{-8}{2} = -4 $ Así:
$$ \dfrac{4x^2 - 8x + 1}{x^3 - x + 6} = \dfrac{3}{x + 2} + \dfrac{x - 4}{x^2 - 2x + 3} $$ Si tomamos valores en (4) tenemos:
$ x = - 2 \Longrightarrow 33 = A 11 \Rightarrow A = 3 $
$ x = 0 \Longrightarrow 1 = 3A + 2C \Rightarrow 1 - 9 = 2C \Rightarrow -8 = 2C \Rightarrow C = -4 $
$ x = 1 \Longrightarrow -3 = 2A + (B + C)3 \Rightarrow -3 = 6 + 3B - 12 \Rightarrow 9 = 6 + 3B \Rightarrow 3 = 3B \Rightarrow B = 1 $
Ejemplo 7: $$ \dfrac{ 2x^2 - x + 4 }{ x^3 + 4x } $$
Solución Se tiene que la fracción se puede descomponer de la siguiente forma:
$$ \dfrac{2x^2 - x + 4}{ x^3 + 4x } = \dfrac{2x^2 - x + 4}{x \left( x^2 + 4 \right) } = \dfrac{A}{x} + \dfrac{Bx + C}{x^2 + 4} $$ De donde se obtiene multiplicando por el común denominador:
$$ 2x^2 - x + 4 = A(x^2 + 4) + (Bx + C)x \qquad (5) $$ $$ 2x^2 - x + 4 = Ax^2 + 4A + Bx^2 + Cx $$ $$ 2x^2 - x + 4 = x^2(A + B) + Cx + 4A$$ $$\left \{ \begin{array}{ll} A + B & = 2 \cr C & = -1 \cr 4A & = 4 \Rightarrow A = 1 \end{array} \right. $$ $$ A + B = 2 \Rightarrow \quad A = 1. $$ Por lo cual $$ \dfrac{2x^2 - x + 4}{x^3 + 4x} = \dfrac{1}{x} + \dfrac{x - 1}{x^2 + 4} $$
Si tomamos valores en (5)
$ x = 0 \Longrightarrow 4 = A 4 \Rightarrow A = 1 $
$ x = 1 \Longrightarrow 5 = A5 + (B + C) \Rightarrow B = -C $
$ x = -1 \Longrightarrow 7 = 5 - (-B + C) \Rightarrow 2 = -2C \Rightarrow C = -1 \Rightarrow B = 1$
Caso IV: El denominador $Q(x)$ contiene un factor irreductible repetido.
Si $Q(x)$ tiene un factor cuadrático repetido $k$ veces de la forma $\left ( ax^2 + bx + c \right )^{k}$, donde $b^2 - 4ac < 0$, entonces la descomposición en fracciones parciales contiene $k$ términos de la forma: $$ \dfrac{ A_{1} x + B_{1}}{ax^2 + bx + c} + \dfrac{A_{2}x + B_2}{\left( ax^2 + bx + c \right)^2} + \cdots + \dfrac{A_{k} x + B_k}{ \left ( ax^2 + bx + c \right)^k} $$ donde $A_1, A_2, \cdots, A_k,$ y $B_1, B_2, \cdots B_k$ son constantes.
Ejemplo 8: Descomponer en fracciones parciales $$ \dfrac{1 - x + 2x^2 - x^3}{x \left( x^2 + 1 \right)^2 } $$ Solución: La forma de descomponer esta division de polinimios en fracciones parciales es: $$ \dfrac{1 - x + 2x^2 - x^3}{ x \left( x^2 + 1 \right )^2 } = \dfrac{A}{x} + \dfrac{Bx + C}{x^2 + 1} + \dfrac{D x + E}{ \left( x^2 + 1 \right )^2 } $$ Multiplicando por $x \left( x^2 + 1 \right)^2$ y luego igualando coeficientes
$$ 1 - x + 2x^2 - x^3 = A( x^2 + 1)^2 + (Bx + C)x(x^2 + 1) + x(Dx + E) \qquad (6) $$ $$ 1 - x + 2x^2 - x^3 = A(x^4 + 2x^2 + 1) + (Bx + C)(x^3 + x) + Dx^2 + Ex $$ $$ 1 - x + 2x^2 - x^3 = A(x^4 + 2x^2 + 1) + Bx^4 + Bx^2 + Cx^3 + Cx + Dx^2 + Ex $$ $$ 1 - x + 2x^2 - x^3 = x^4(A + B) + x^3C + x^2(2A + B + D) + x(C + E) + A $$ se obtiene el siguiente sistema: $$\left \{ \begin{array}{ll} A + B & = 0 \cr C & = -1 \cr 2A + B + D & = 2 \cr C + E & = -1 \cr A & = 1 \cr \end{array} \right. $$ Cuya solución es: $ A = 1$, como $ B = -A \Rightarrow B = -1$, como $ C = -1 \Rightarrow E = 0$ y así $ D = 1 $.
Entonces $$ \dfrac{1 - x + 2x^2 - x^3 }{x \left ( x^2 + 1 \right )^2 } = \dfrac{1}{x} - \dfrac{x + 1}{x^2 + 1} + \dfrac{x}{\left( x^2 + 1 \right )^2 } $$
Tomando valores en (6) tenemos:
$ x = 0 \Longrightarrow 1 = A $
$ x = 1 \Longrightarrow 1 = 4A + 2(B + C) + (D + E) \Rightarrow - 3 = 2B + 2C + D + E $
$ x = -1 \Longrightarrow 5 = 4A - 2(B + C) - (-D + E) \Rightarrow 1 = 2B - 2C + D - E $
$ x = 2 \Longrightarrow -1 = 25A + 10(2B + C) + 2(2D + E) \Rightarrow -26 = 20B + 10C + 4D + 2E $
$ x = -2 \Longrightarrow 19 = 25A - 10(2B + C) - 2(-2D + E) \Rightarrow -6 = 20B - 10C + 4D - 2E $
se obtiene el siguiente sistema: $$\left \{ \begin{array}{ll} 2B + 2C + D + E & = -3 \cr 2B - 2C + D - E & = 1 \cr 20B + 10C + 4D + 2E & = -26 \cr 20B - 10C + 4D - 2E & = -6 \cr \end{array} \right. $$ Sumamos la $1^{\underline{a}}$ y $2^{\underline{a}}$ ecuación y tenemos: (a) $-1 = 2B + D$
Sumamos la $3^{\underline{a}}$ y $4^{\underline{a}}$ ecuación y tenemos: (b) $-4 = 5B + D$
Restamos $(a)$ y $(b): 3 = -3B \Rightarrow B = -1 \Rightarrow D = 1$
Restamos la $1^{\underline{o}}$ y $2^{\underline{a}}$ ecuación y tenemos: (c) $-2 = 2C + E$
Restamos la $3^{\underline{a}}$ y $4^{\underline{a}}$ ecuación y tenemos: (d) $-5 = 5C + E$
Restamos $(c)$ y $(d): 3 = -3C \Rightarrow C = -1 \Rightarrow E = 0$
Ejemplo 9: $$ \dfrac{x^3}{x^4 + 4x^2 + 4}$$ Solución La forma de descomponer esta division de polinimios en fracciones parciales es: $$ \dfrac{x^3}{x^4 + 4x^2 + 4} = \dfrac{Ax + B}{x^2 + 2} + \dfrac{Cx + D}{ (x^2 + 2)^2 } $$
Multiplicando por el mínimo común múltiplo y luego igualando coeficientes
$$ x^3 = (Ax + B)(x^2 + 2) + (Cx + D) \qquad (7) $$
$$ x^3 = Ax^3 + 2Ax + Bx^2 + 2B + Cx + D $$
$$ x^3 = Ax^3 + Bx^2 + x(2A + C) + 2B + D $$
se obtiene el siguiente sistema: $$\left \{ \begin{array}{ll} A & = 1 \cr B & = 0 \cr 2A + C & = 0 \Rightarrow C = -2\cr 2B + D & = 0 \Rightarrow D = 0 \cr \end{array} \right. $$ En este caso no merece la pena tomar valores en $x$, pero ser puede hacer sin problemas.






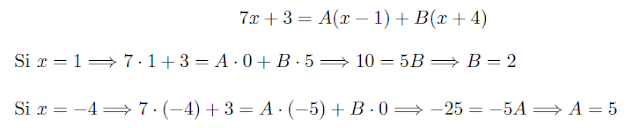





1 comentario:
Holaa Rafa,
Un pregunta, el caso en que al descomponer el denominador se obtenga un polinomio de la forma 1+x^2, está subido?
¿Por qué en ese caso el denominador tiene que ser de la forma Bx+C?
Soy Olga, tu exalumna xdd
Publicar un comentario