Ecuaciones de primer grado, con paréntesis y denominadores.

LOS NUMERALES MULTIPLICATIVOS (1-13 y 100): «Los numerales multiplicativos expresan multiplicación».

• (x2): doble, duplo/pla,
• (x3): triple, triplo/pla,
• (x4): cuádruple, cuádruplo/pla,
• (x5): quíntuple, quíntuplo/pla,
• (x6): séxtuple, séxtuplo/pla,
• (x7): séptuple, séptuplo/pla,
• (x8): óctuple, óctuplo/pla,
• (x9): nónuplo/pla,
• (x10): décuplo/pla,
• (x11): undécuplo/pla,
• (x12): duodécuplo/pla,
• (x13): terciodécuplo/pla,
• (x14): cuartodécuplo/pla,
• (x15): quintodécuplo/pla,
• (x16): sextodécuplo/pla,
• (x100): céntuplo/pla.

(*) Del 14 al 99 los multiplicativos en español son inusitados, por lo que, en su lugar, se suelen emplear las expresiones « $X$ veces mayor» o "$X$ veces más".



¿Qué es una ecuación? Es una igualdad en las que aparecen números y letras (llamadas incógnitas) relacionados mediante operaciones matemáticas. En las ecuaciones distinguimos varios elementos:

• Incógnita: La letra o variable que aparece en la ecuación, normalmente es la letra $x$ pero puede ser cualquiera.


• Miembro: Es cada una de las dos expresiones algebraicas separadas por el signo «=».


• Término: Cada uno de los sumandos que componen los miembros de la ecuación.


• Grado: Es el mayor de los exponentes de las incógnitas, en esta entrada es 1, ecuaciones de $\odn{1}{er}$ grado.

Vamos a resolver diferentes tipos de ecuaciones de $\odn{1}{er}$ grado, con paréntesis y con denominadores. Para ellos vamos a repasar algunas cosas:

Ecuación equivalente: «Aquellas ecuaciones que tienen las mismas soluciones.»

Regla de la suma: «Si a los dos miembros de una ecuación, les sumamos o restamos el mismo número o la misma expresión algebraica, obtenemos una ecuación equivalente.»

Regla del producto: «Si multiplicamos o dividimos los dos miembros de la ecuación por el mismo número distinto de cero, obtenemos una ecuación equivalente.»



Para resolver ecuaciones de $\odn{1}{er}$ grado sin paréntesis y sin denominadores lo que haremos será seguir los siguientes pasos:

1. Agruparemos términos en cada uno de los miembros de la ecuación


2. Transpondremos términos, los que tienen $x$ a un lado y los números a otro (usaremos la Regla de la suma)


3. Agrupamos de nuevo términos


4. Despejamos la $x$ (usaremos la Regla del producto)


5. Comprobamos la solución

Ecuaciones de $\odn{1}{er}$ grado, sin paréntesis y sin denominadores.

En este ejercicio no podemos agrupar en cada miembro de la ecuación, luego directamente trasponemos los términos, es decir, pasamos las $x$ a un lado y los números al otro:
$$ 5x - 7 = 2 - 4x $$
$$ 5x + 4x = 2 + 7 $$
$$ 9x = 9 $$
$$ x = \dfrac{\ 9\ }{9} = 1 $$
Una vez solucionada la ecuación,siempre debemos comprobar la misma, siempre en la ecuación original:

$ 5 \cdot 1 - 7 = 2 - 4 \cdot 1 \Rightarrow 5 -7 = 2 - 4 \Rightarrow -2 = -2 \checkmark$

En esta ecuación podemos agrupar términos en cada miembro de la ecuación, antes de transponer dichos términos:
$$ 3x + x + 4 = 2x + 10 $$
$$ 4x + 4 = 2x + 10 $$
$$ 4x - 2x = 10 - 4 $$
$$ 2x = 6$$
$$ x = \dfrac{\ 6\ }{2} = 3 $$
Ahora comprobamos la ecuación, sustituimos $x$ por 3 y vemos que la ecuación se cumple:

$ 3 \cdot 3 + 3 + 4 = 2 \cdot 3 + 10 \Rightarrow 9 + 7 = 6 + 10 \Rightarrow = 16 = 16 \checkmark $

Agrupamos términos en cada uno de los miembros de la ecuación: $$ 6x - 9 + 3x - 2 - 5x = x - 6 - 3x + 1 $$
Trasponemos los términos, las $x$ a la izquierda de la ecuación ya que el coeficiente quedará positivo: $$ 4x - 11 = - 2x - 5 $$
Agrupamos de nuevo: $$ 4x + 2x = 11 - 5 $$
$$ 6x = 6 $$
Despejamos: $$ x = \dfrac{\ 6\ }{6} = 1 $$
Ahora comprobamos la ecuación, sustituimos $x$ por 1 y vemos que la ecuación se cumple:

$ 6 \cdot 1 - 9 + 3 \cdot 1 - 2 - 5 \cdot 1 = 1 - 6 - 3 \cdot 1 + 1 $
$ 6 - 9 + 3 - 2 - 5 = 1 - 6 - 3 + 1 $
$ -3 + 3 - 7 = -5 - 2 $
$ - 7 = - 7 \checkmark $

En esta ecuación podemos agrupar términos en cada miembro de la ecuación, antes de transponer dichos términos:
$$ 3x - x + 7x + 12 = 3x + 9 - x + 4x + 18 $$
$$ 9x + 12 = 6x + 27 $$
Transponemos términos: $$ 9x - 6x = 27 - 12 $$
Agrupamos de nuevo: $$ 3x = 15 $$
Despejamos: $$ x = \dfrac{\ 15\ }{3} = 5 $$
Ahora comprobamos la ecuación, sustituimos $x$ por 5 y vemos que la ecuación se cumple:

$ 3 \cdot 5 - 5 + 7 \cdot 5 + 12 = 3 \cdot 5 + 9 - 5 + 4 \cdot 5 + 18 $
$ 15 - 5 + 35 + 12 = 15 + 9 - 5 + 20 + 18 $
$ 57 = 57 \checkmark $

Ecuaciones de $\odn{1}{er}$ grado con paréntesis y sin denominadores.

Para ello recordaremos como se trabaja los paréntesis, aplicando la propiedad distributiva: $$ a \times (b + c) = a \times b + a \times c \qquad \text{ y } \qquad a \times (b - c) = a \times b - a \times c $$ y la regla de los signos: $$ \oplus = \oplus \times \oplus \qquad \oplus = \ominus \times \ominus $$ $$ \ominus = \oplus \times \ominus \qquad \ominus = \ominus \times \oplus $$
Veamos unos ejemplos:

$ 3 \cdot ( 2x + 3) = 3 \cdot 2x + 3 \cdot 3 = 6x + 9 $	$ 2 \cdot (-4 - x ) = 2 \cdot (-4) - 2 \cdot x = -8 - 2x $
$ 9 \cdot ( -x + 7) = 9 \cdot (-x) + 9 \cdot 7 = -9x + 63 $	$ 5 \cdot (1 - 2x ) = 5 \cdot 1 - 5 \cdot 2x = 5 - 10x $
$ -4 \cdot ( 3x + 5) = -4 \cdot 3x + (-4) \cdot 5 = -12x -20 $	$ -7 \cdot (-1 - 2x ) = (-7) \cdot (-1) - (-7) \cdot 2x = 7 + 14x $
$ -8 \cdot ( -2x + 3) = -8 \cdot (-2x) + (-8) \cdot 3 = 16x -24 $	$ - 11 \cdot ( 2 - 3x ) = (-11) \cdot 2 - (-11) \cdot 3x = -22 + 33x $

Podemos usar estas tablas para entender la aplicación de la propiedad distributiva:

Recordemos además que:

$$ - (3 + x) = (-1) \cdot (3 + x) = (-1) \cdot 3 + (-1) \cdot x = - 3 - x $$

$$ - (2x - 7) = (-1) \cdot (2x - 7) = (-1) \cdot 2x - (-1) \cdot 7 = - 2x + 7 $$

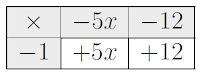
$$ - (- 5x - 12) = (-1) \cdot (-5x - 12) = (-1) \cdot (-5x) - (-1) \cdot 12 = 5x + 12 $$

Para resolver ecuaciones de $\odn{1}{er}$ grado con paréntesis y sin denominadores lo que haremos será seguir los siguientes pasos:

1. Quitar los paréntesis. ¡¡Cuidado con los signos negativos delante del paréntesis y con los signos negativos que están dentro del paréntesis!!


2. Agruparemos términos en cada uno de los miembros de la ecuación


3. Transpondremos términos, los que tienen $x$ a un lado y los números a otro (Regla de la suma)


4. Agrupamos de nuevo términos


5. Despejamos la $x$ (Regla del producto)


6. Comprobamos la solución

Quitamos los paréntesis $$ 2x + 3 \cdot (2x - 1) = x + 67 $$
$$ 2x + 3 \cdot 2x - 3 \cdot 1 = x + 67 $$
$$ 2x + 6x - 3 = x + 67 $$
Ahora ya tenemos una ecuación de $\odn{1}{er}$ grado sin paréntesis y sabemos resolverla: $$ 2x + 6x - 3 = x + 67 $$
Agrupamos términos: $$ 8x - 3 = x + 67 $$
Transponemos términos: $$ 7x = 70 $$
$$ x = \dfrac{\ 70\ }{7} = 10 $$
Ahora comprobamos la ecuación, sustituimos $x$ por 10 y vemos que la ecuación se cumple:

$ 2 \cdot 10 + 3 \cdot (2 \cdot 10 - 1) = 10 + 67 $
$ 20 + 3 \cdot 19 = 77 $
$ 20 + 57 = 77 \checkmark $

Quitamos los paréntesis aplicando la propiedad distributiv y teniendo cuidado con los signos:
$$ 3 \cdot (12 - x) - 4x = 2 \cdot (11 - x) + 9x $$
$$ 3 \cdot 12 - 3 \cdot x - 4x = 2 \cdot 11 - 2 \cdot x + 9x $$
$$ 36 - 3x - 4x = 22 - 2x + 9x $$
Ya tenemos una ecuación sin paréntesis que ya sabemos resolver, vamos a agrupar en cada uno de los miembros: $$ 36 - 7x = 22 + 7x $$
Ahora transponemos términos, en este caso pasamos las $x$ a la derecha para qué quede positiva: $$ 36 - 22 = 7x + 7x $$
Volvemos a agrupar y despejamos: $$ 14 = 14x $$
$$ x = \dfrac{\ 14\ }{14} = 1 $$
Ahora comprobamos la ecuación, sustituimos $x$ por 1 y vemos que la ecuación se cumple:

$ 3 \cdot (12 - 1) - 4 \cdot 1 = 2 \cdot (11 - 1) + 9 \cdot 1 $
$ 3 \cdot 11 - 4 = 2 \cdot 10 + 9 $
$ 33 - 4 = 20 + 9 $
$ 29 = 29 \checkmark $

Vamos a quitar los paréntesis y teniendo cuidado con los signos negativos: $$ 3 \cdot (x + 7) = - (5 - x) + 6 $$
$$ 3 \cdot x + 3 \cdot 7 = - 5 + x + 6 $$
$$ 3x + 21 = - 5 + x + 6 $$
Tenemos una ecuación de $\odn{1}{er}$ grado sin paréntesis que ya sabemos resolver, agrupamos términos en cada miembro de la ecuación:
$$ 3x + 21 = x + 1 $$
Transponemos términos y despejamos: $$ 3x - x = 1 - 21 $$
$$ 2x = - 20 $$
$$ x = \dfrac{\ - 20\ }{2} = -10 $$ Ahora comprobamos la ecuación, sustituimos $x$ por -10 y vemos que la ecuación se cumple:

$ 3 \cdot (-10 + 7) = - (5 - (-10)) + 6 $
$ 3 \cdot (-3) = - (5 + 10) + 6 $
$ - 9 = - 15 + 6 $
$ - 9 = - 9 \checkmark $

Quitamos los paréntesis teniendo cuidado con los signos negativos: $$ 2x + 3 \cdot (x + 1) = 11 - 2 \cdot (2x - 5) $$ $$ 2x + 3 \cdot x + 3 \cdot 1 = 11 - 2 \cdot 2x - (-2) \cdot 5 $$ $$ 2x + 3x + 3 = 11 - 4x + 10 $$ Ahora tenemos una ecuación si paréntesis que sabemos resolver,, agrupamos términos y tenemos:
$$ 5x + 3 = 21 - 4x $$ Transponemos términos y despejamos: $$ 5x + 4x = 21 - 3 $$ $$ 9x = 18 $$ $$ x = \dfrac{\ 18\ }{9} = 2 $$ Ahora comprobamos la ecuación, sustituimos $x$ por 2 y vemos que la ecuación se cumple:

$ 2 \cdot 2 + 3 \cdot (2 + 1) = 11 - 2 \cdot (2 \cdot 2 - 5) $
$ 4 + 3 \cdot 3 = 11 - 2 \cdot (4 - 5) $
$ 4 + 9 = 11 - 2 \cdot (-1) $
$ 13 = 11 + 2 \checkmark $

Quitamos los paréntesis teniendo mucho cuidado con los signos negtivos:
$$ 5x - 3 \cdot (2x - 1) - (x + 5) = -4 - 2 \cdot (3x + 5) $$ $$ 5x - 3 \cdot 2x - (-3) \cdot 1 - x - 5 = -4 - 2 \dot 3x + (-2) \cdot 5 $$ $$ 5x - 6x + 3 - x - 5 = -4 - 6x - 10 $$ Tenemos una ecuación sin paréntesis que ya sabemos resolver, agrupamos en cada uno de los miembros:
$$ -2x - 2 = - 6x - 14 $$ Transponemos términos y despejamos: $$ 6x - 2x = 2 - 14 $$ $$ 4x = - 12 $$ $$ x = \dfrac{\ -12\ }{4} = - 3 $$ Ahora comprobamos la ecuación, sustituimos $x$ por -3 y vemos que la ecuación se cumple:

$ 5 \cdot (-3) - 3 \cdot (2 \cdot (-3) - 1) - (-3 + 5) = -4 - 2 \cdot (3 \cdot (-3) + 5) $
$ -15 - 3 \cdot (-6 - 1) - (2) = -4 - 2 \cdot (-9 + 5) $
$ -15 - 3 \cdot (-7) - 2 = -4 - 2 \cdot (-4) $
$ -15 + 21 - 2 = -4 + 8 $
$ 4 = 4 \checkmark $

Quitamos los paréntesis con mucho cuidado con los signos negativos:
$$ 3 \cdot [ x + (14 - x) ] = 2 \cdot [x - (2x - 21)] $$ $$ 3 \cdot x + 3 \cdot (14 - x) ] = 2 \cdot x - 2 \cdot (2x - 21) $$ $$ 3 \cdot x + 3 \cdot 14 - 3 \cdot x = 2 \cdot x - 2 \cdot 2x - (-2) \cdot 21 $$ $$ 3x + 42 - 3x = 2x - 4x + 42 $$ Ahora tenemos una ecuación sin paréntesis, agrupamos los términos en los dos miembros de la ecuación:
$$ 42 = -2x + 42 $$ Transponemos términos y despejamos: $$ 2x = 42 - 42 $$ $$ 2x = 0 \Rightarrow x = 0 $$ Ahora comprobamos la ecuación, sustituimos $x$ por 0 y vemos que la ecuación se cumple:

$ 3 \cdot [ 0 + (14 - 0) ] = 2 \cdot [0 - (2 \cdot 0 - 21)] $
$ 3 \cdot 14 = 2 \cdot 21 $
$ 42 = 42 \checkmark $

Ecuaciones de $\odn{1}{er}$ grado con paréntesis y con denominadores.

Para resolver ecuaciones de $\odn{1}{er}$ grado con paréntesis y con denominadores lo que haremos será seguir los siguientes pasos:

1. Calcular el mínimo común múltiplo de todos los denominadores de las fracciones que hay en la ecuación.


2. Multiplicar los dos miembros de la ecuación por el mínimo común múltiplo calculado anteriormente, aplicamos la distributiva y quitamos los denominadores. Ahora tenemos una ecuación con paréntesis que ya sabemos resolver.


3. Quitar los paréntesis. ¡¡Cuidado con los signos negativos delante del paréntesis y con los signos negativos que están dentro del paréntesis!!


4. Agruparemos términos en cada uno de los miembros de la ecuación


5. Transpondremos términos, los que tienen $x$ a un lado y los números a otro (Regla de la suma)


6. Agrupamos de nuevo términos


7. Despejamos la $x$ (Regla del producto)


8. Comprobamos la solución

Lo primero recordar que $ \dfrac{\ 1\ }{2} x = \dfrac{\ x\ }{2} $. Ahora calculamos el mínimo común múltiplo de los denominadores, como sólo está el 2, en este caso es muy fácil, multiplicaremos los dos miembros de la ecuación por 2: $$ 3x + \dfrac{\ 1\ }{2} x + 6 = 2x $$ $$ 2 \cdot \left ( 3x + \dfrac{\ 1\ }{2} x + 6 \right ) = 2 \cdot 2x $$ Aplicamos la propiedad distributiva y quitamos los denominadores: $$ 2 \cdot 3x + 2 \cdot \dfrac{\ 1\ }{2} x + 2 \cdot 6 = 2 \cdot 2x $$ $$ 6x + x + 12 = 4x $$ Ahora tenemos una ecuación sin paréntesis y sin denominadores que ya sabemos resolver, agrupamos, transponemos, agrupamos y despejamos: $$ 7x + 12 = 4x $$ $$ 3x = - 12 $$ $$ x = \dfrac{\ - 12\ }{3} = - 4 $$ Ahora comprobamos la ecuación, sustituimos $x$ por -4 y vemos que la ecuación se cumple:

$ 2 \cdot 3 \cdot (-4) + 2 \cdot \dfrac{\ 1\ }{2} \cdot (-4) + 2 \cdot 6 = 2 \cdot 2 \cdot (-4) $
$ -24 - 4 + 12 = -16 $
$ - 16 = 16 \checkmark $$

El mínimo común múltiplo de los denominadores es 6, luego multiplicamos ambos miembros de la ecuación por 6 y aplicamos la propiedad distributiva: $$ \dfrac{\ x\ }{3} - \dfrac{\ 7\ }{2} = \dfrac{\ 5\ }{2} $$
$$ 6 \cdot \left ( \dfrac{\ x\ }{3} - \dfrac{\ 7\ }{2} \right ) = 6 \cdot \left ( \dfrac{\ 5\ }{2} \right ) $$
$$ 6 \cdot \dfrac{\ x\ }{3} - 6 \cdot \dfrac{\ 7\ }{2} = 6 \cdot \dfrac{\ 5\ }{2} $$
$$ 2x - 21 = 15 $$ Ya tenemos una ecuación de $\odn{1}{er}$ sin paréntesis y sin denominadores que ya sabemos resolver: $$ 2x = 36 $$ $$ x = \dfrac{\ 36\ }{2} = 18 $$ En este caso podíamos haberlo hecho de otra forma, transponemos términos y nos queda: $$ \dfrac{\ x\ }{3} - \dfrac{\ 7\ }{2} = \dfrac{\ 5\ }{2} $$
$$ \dfrac{\ x\ }{3} = \dfrac{\ 7\ }{2} + \dfrac{\ 5\ }{2} $$
$$ \dfrac{\ x\ }{3} = \dfrac{\ 12\ }{2} $$
$$ \dfrac{\ x\ }{3} = 6 $$
Despejamos la $x$ nos queda que $x = 6 \cdot 3 = 18$
Ahora comprobamos la ecuación, sustituimos $x$ por 18 y vemos que la ecuación se cumple:

$ \dfrac{\ 18\ }{3} - \dfrac{\ 7\ }{2} = \dfrac{\ 5\ }{2} $
$ 6 = \dfrac{\ 7\ }{2} + \dfrac{\ 5\ }{2} $
$ 6 = \dfrac{\ 12\ }{2} \checkmark $

El mínimo común múltiplo de los denominadores es 12, luego multiplicamos ambos miembros de la ecuación por 6 y aplicamos la propiedad distributiva: $$ \dfrac{\ 5x + 7\ }{2} - \dfrac{\ 3x + 9\ }{4} = \dfrac{\ 2x + 5\ }{3} + 5 $$ $$ 12 \cdot \left ( \dfrac{\ 5x + 7\ }{2} - \dfrac{\ 3x + 9\ }{4} \right ) = 12 \cdot \left ( \dfrac{\ 2x + 5\ }{3} + 5 \right ) $$ $$ 12 \cdot \dfrac{\ 5x + 7\ }{2} - 12 \cdot \dfrac{\ 3x + 9\ }{4} = 12 \cdot \dfrac{\ 2x + 5\ }{3} + 12 \cdot 5 $$ Para entenderlo ponemos que el mínimo común múltiplo multiplica al numerador de cada fracción $$ \dfrac{\ 12 \cdot ( 5x + 7)\ }{2} - \dfrac{\ 12 \cdot (3x + 9)\ }{4} = \dfrac{\ 12 \cdot ( 2x + 5) \ }{3} + 12 \cdot 5 $$ Simplificando nos queda: $$ \dfrac{\ \cancelto{6}{12} \cdot ( 5x + 7)\ }{ \cancel{2} } - \dfrac{\ \cancelto{3}{12} \cdot (3x + 9)\ }{ \cancel{4} } = \dfrac{\ \cancelto{4}{12} \cdot ( 2x + 5) \ }{ \cancel{3} } + 12 \cdot 5 $$ $$ 6 \cdot (5x + 7) - 3 \cdot ( 3x + 9) = 4 \cdot ( 2x + 5 ) + 12 \cdot 5 $$ Ahora tenemos una ecuación con paréntesis que ya sabemos hacer. Quitamos los paréntesis teniendo cuidado con los signos negativos: $$ 6 \cdot 5x + 6 \cdot 7 - 3 \cdot 3x + (-3) \cdot 9 = 4 \cdot 2x + 4 \cdot 5 + 60 $$ $$ 30x + 42 - 9x - 27 = 8x + 20 + 60 $$ Agrupamos, transponemos y volvemos a agrupar términos y despejamos: $$ 21x + 15 = 8x + 80 $$ $$ 13x = 65 $$ $$ x = \dfrac{\ 65\ }{13} = 5 $$ Ahora comprobamos la ecuación, sustituimos $x$ por 18 y vemos que la ecuación se cumple:

$ \dfrac{\ 5 \cdot 5 + 7\ }{2} - \dfrac{\ 3 \cdot 5 + 9\ }{4} = \dfrac{\ 2 \cdot 5 + 5\ }{3} + 5 $

$ \dfrac{\ 32\ }{2} - \dfrac{\ 24\ }{4} = \dfrac{\ 15\ }{3} + 5 $

$ 16 - 6 = 5 + 5 $

$ 10 = 10 \checkmark $

El mñinimo común múltiplo de los denominadores es 15, luego multiplicamos ambos miembros de la ecuación por 15 y aplicamos la propiedad distributiva: $$ \dfrac{\ 2 \cdot (x - 2)\ }{3} - x + 2 = \dfrac{\ 3 \cdot (- x - 2)\ }{5} $$ $$ 15 \cdot \left ( \dfrac{\ 2 \cdot (x - 2)\ }{3} - x + 2 \right ) = 15 \cdot \left ( \dfrac{\ 3 \cdot (- x - 2)\ }{5} \right ) $$ $$ \dfrac{\ 15 \cdot 2 \cdot (x - 2) \ }{3} - 15 \cdot x + 15 \cdot 2 = \dfrac{\ 15 \cdot 3 \cdot (- x - 2)\ }{5} $$ Simplificamosy nos quedará una ecuación con paréntesis que ya sabemos resolver: $$ \dfrac{\ \cancelto{5}{15} \cdot 2 \cdot (x - 2) \ }{ \cancel{3} } - 15 \cdot x + 15 \cdot 2 = \dfrac{\ \cancelto{3}{15} \cdot 3 \cdot (- x - 2)\ }{ \cancel{5} } $$ $$ 5 \cdot 2 \cdot (x - 2) - 15x + 30 = 3 \cdot 3 \cdot (- x - 2) $$ $$ 10 \cdot (x - 2) - 15x + 30 = 9 \cdot (- x - 2) $$ $$ 10 \cdot x - 10 \cdot 2 - 15x + 30 = 9 \cdot (- x) - 9 \cdot 2 $$ $$ 10x - 20 - 15x + 30 = -9x - 18 $$ Ya tenemos una euación sin paréntesis y sin denominadores que ya sabemos hacer, agrupamos, transponemos términos y despejamos: $$ - 5x + 10 = -9x - 18 $$ $$ - 5x + 9x = -10 - 18 $$ $$ 4x = - 28 $$ $$ x = \dfrac{\ - 28\ }{4} = - 7 $$ Ahora comprobamos la ecuación, sustituimos $x$ por -7 y vemos que la ecuación se cumple:

$ \dfrac{\ 2 \cdot (-7 - 2)\ }{3} - (-7) + 2 = \dfrac{\ 3 \cdot (- (-7) - 2)\ }{5} $

$ \dfrac{\ 2 \cdot (-9)\ }{3} + 7 + 2 = \dfrac{\ 3 \cdot (7 - 2)\ }{5} $

$ 2 \cdot (-3) + 7 + 2 = \dfrac{\ 3 \cdot 5 \ }{5} $

$ -6 + 9 = 3 \checkmark $

El mínimo común mútiplo de los denominadores es 60, luego multiplicamos los dos miembros de la ecuación por 60 y apicamos la propiedad distributiva: $$ 60 \cdot \left ( \dfrac{\ 5x\ }{3} - 3 \left ( \dfrac{\ x\ }{4} + \dfrac{\ 4\ }{5} \right ) \right ) = 60 \cdot \left ( 3 \left ( \dfrac{\ 1\ }{5} - \dfrac{\ 2x\ }{3} \right ) - 38 \right ) $$ $$ 60 \cdot \dfrac{\ 5x\ }{3} - 60 \cdot 3 \left ( \dfrac{\ x\ }{4} + \dfrac{\ 4\ }{5} \right ) = 60 \cdot 3 \left ( \dfrac{\ 1\ }{5} - \dfrac{\ 2x\ }{3} \right ) - 60 \cdot 38 $$ $$ 60 \cdot \dfrac{\ 5x\ }{3} - 180 \cdot \dfrac{\ x\ }{4} - 180 \cdot \dfrac{\ 4\ }{5} = 180 \cdot \dfrac{\ 1\ }{5} - 180 \cdot \dfrac{\ 2x\ }{3} - 60 \cdot 38 $$ $$ \dfrac{\ 60 \cdot 5x\ }{3} - \dfrac{\ 180 \cdot x\ }{4} - \dfrac{\ 180 \cdot 4\ }{5} = \dfrac{\ 180 \ }{5} - \dfrac{\ 180 \cdot 2x\ }{3} - 60 \cdot 38 $$ $$ \dfrac{\ \cancelto{20}{60} \cdot 5x\ }{ \cancel{3} } - \dfrac{\ \cancelto{45}{180} \cdot x\ }{ \cancel{4} } - \dfrac{\ \cancelto{36}{180} \cdot 4\ }{ \cancel{5} } = \dfrac{\ \cancelto{36}{180} \ }{ \cancel{5} } - \dfrac{\ \cancelto{60}{180} \cdot 2x\ }{ \cancel{3} } - 60 \cdot 38 $$ $$ 100x - 45 x - 144 = 36 - 120x - 1680 $$ Tenemos una ecuación sin paréntesis y sin denominadores que sabemos hacer, agrupamos, transponemos, agrupamos y despejamos: $$ 100x - 45 x - 144 = 36 - 120x - 2280 $$ $$ 55x - 144 = - 120x - 2244 $$ $$ 55x + 120x = + 144 - 2244 $$ $$ 175x = -2100 $$ $$ x = \dfrac{\ -2100\ }{175} = -12 $$ Ahora comprobamos la ecuación, sustituimos $x$ por -12 y vemos que la ecuación se cumple:

$ \dfrac{\ 5 \cdot (-12)\ }{3} - 3 \left ( \dfrac{\ -12\ }{4} + \dfrac{\ 4\ }{5} \right ) = 3 \left ( \dfrac{\ 1\ }{5} - \dfrac{\ 2 \cdot (-12)\ }{3} \right ) - 38 $

$ - 20 - 3 \left ( -3 + \dfrac{\ 4\ }{5} \right ) = 3 \left ( \dfrac{\ 1\ }{5} - (-8) \right ) - 38 $

$ - 20 - 3 \left ( \dfrac{\ -11\ }{5} \right ) = 3 \left ( \dfrac{\ 41\ }{5} \right ) - 38 $

$ \dfrac{\ 33\ }{5} - \left ( \dfrac{\ 123\ }{5} \right ) = 20 - 38 $

$ - \left ( \dfrac{\ 90\ }{5} \right ) = - 18 $

$ - 18 = - 18 \checkmark $

Iremos actualizando esta sección con los ejercicios que nos pidáis, para ello podéis mandar un correo a profesor.maties@gmail.com