Continuidad y tipos de discontinuidad de funciones

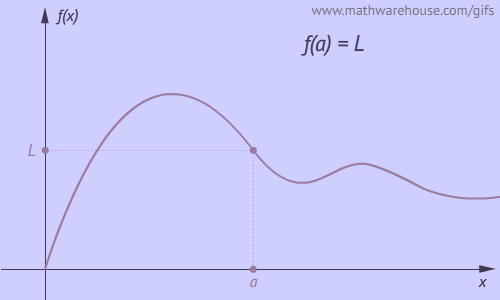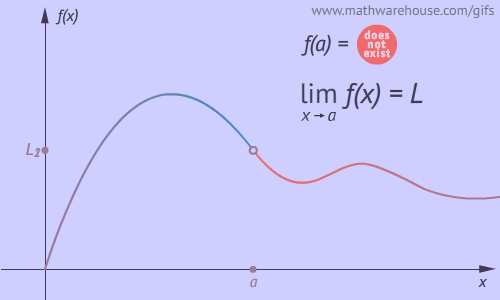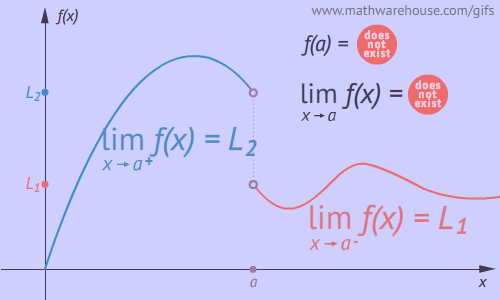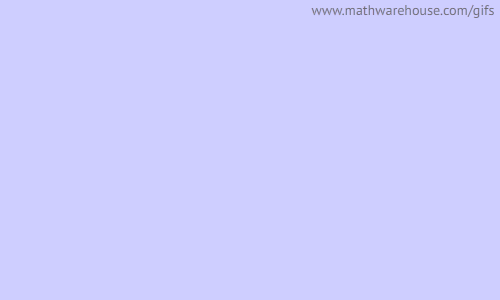
Vemos explicado gráficamente los diferentes tipos de discontinuidades que se pueden dar. Gráfico obtenido de la siguiente web. 

  

Para que una función sea continua en $x=a$ tiene que cumplirse: 

1. $\mathrm{\exists }{\displaystyle \underset{x\to a}{lim}f(x)\iff {\displaystyle \underset{x\to a^{+}}{lim}f(x)={\displaystyle \underset{x\to a^{-}}{lim}f(x)}}}$ 
2. $\mathrm{\exists }f(a)$
3. ${\displaystyle \underset{x\to a}{lim}f(x)=f(a)}$ 

Si la condición 2 no se cumple, se dice que la función tiene una discontinuidad evitable, ya que podemos definir una nueva función cuyo valor en $x=a$ sea el ${\displaystyle \underset{x\to a}{lim}f(x)}$. 

Por ejemplo, la función $f(x)={\displaystyle \frac{x^2-1}{x-1}}$ cuyo dominio son todos los reales excepto el 1. $Domf(x)=\mathbb{R}\setminus \{1\}$. En esta función no existe f(1), pero el límite cuando x tiende a 1 sí que existe: 

$${\displaystyle \underset{x\to 1}{lim}{\displaystyle \frac{x^2-1}{x-1}}={\displaystyle \frac{0}{0}}={\displaystyle \underset{x\to 1}{lim}{\displaystyle \frac{(x-1)\cdot (x+1)}{x-1}}={\displaystyle \underset{x\to 1}{lim}(x+1)=2}}}$$

Definimos $F(x)=\{\begin{array}{l}{\displaystyle \frac{x^2-1}{x-1}}\text{ si }x\ne 2\\ \\ 2\text{ si }x=2\end{array}$ 

$F(x)$ es una función continua, cumple las 3 condiciones que hemos comentado anteriormente. 

Las discontinuidades que no son evitables se dividen en tipos, de primera especie o de segunda. Las de primera especie o de primer orden si los límites laterales son distintos o uno de ellos es infinito. Las de segunda especie o de segundo orden si al menos en uno de los lados del punto, la función no existe o no tienen límite.

Discontinuidades de $1^{\underset{―}{a}}$ especie o de $1^{\underset{―}{er}}$ orden:

$${\displaystyle \underset{x\to a^{+}}{lim}f(x)\ne {\displaystyle \underset{x\to a^{-}}{lim}f(x)}}$$

$$\text{ salto }=\left|{\displaystyle \underset{x\to a^{+}}{lim}f(x)-{\displaystyle \underset{x\to a^{-}}{lim}f(x)}}\right|$$

Nota: $f(a)$ puede estar definida o no y puede coincidir o no con alguno de los límites laterales si es finito.

Ejemplo de funciones de $1^{\underset{―}{a}}$ especie o de $1^{\underset{―}{er}}$ orden: 

• de salto finito: $f(x)={\displaystyle \frac{|x|}{x}}$ y ${\displaystyle \underset{x\to 1^{-}}{lim}{\displaystyle \frac{|x|}{x}}=-1}$ y ${\displaystyle \underset{x\to 1^{+}}{lim}{\displaystyle \frac{|x|}{x}}=1}$ 
• de salto infinito: $f(x)=\{\begin{array}{l}{\displaystyle \frac{1}{x}}\text{ si }x<0{\displaystyle \underset{x\to 0^{-}}{lim}{\displaystyle \frac{1}{x}}=-\mathrm{\infty }}\\ \\ x\text{ si }x\ge 0{\displaystyle \underset{x\to 0^{+}}{lim}x=0}\end{array}$ 
• asintótica: $f(x)={\displaystyle \frac{1}{x}}$ con los límites laterales ${\displaystyle \underset{x\to 0^{-}}{lim}{\displaystyle \frac{1}{x}}=-\mathrm{\infty }}$ y ${\displaystyle \underset{x\to 0^{+}}{lim}{\displaystyle \frac{1}{x}}=+\mathrm{\infty }}$

Discontinuidades de $2^{\underset{―}{a}}$ especie o de $2^{\underset{―}{er}}$ orden:

Una función $f(x)$ tiene una discontinuidad de este tipo si no existe alguno de los límites laterales o la función no está definida. 

Nota: $f(a)$ puede estar definida o no.

Ejemplo: $f(x)=\sin \left({\displaystyle \frac{1}{x}}\right)$