Teoremas del seno, coseno y de la tangente

 Teorema del seno:

Para entender mejor el teorema del seno necesitamos 3 resultados geométricos: 

1.- Dos ángulos inscritos en una circunferencia que abarcan el mismo arco son iguales. 

2.- Todo ángulo inscrito en una semicircunferencia es recto. 

Teorema del seno: 

El teorema del seno es una proporción entre las longitudes de los lados de un triángulo y los senos de sus correspondientes ángulos opuestos

$$ \Large \textcolor{blue}{ \fbox{ $ \array{ \cr \quad \mathbf{ \dfrac{a}{\sen \hat{A}} = \dfrac{b}{\sen \hat{B}} = \dfrac{c}{\sen \hat{C} } = 2R} \quad \cr \quad } $ } } $$

donde $R$ es el radio de la circunferencia circunscrita al triángulo $\triangle{ABC}$.

Teorema del coseno: 

Teorema del coseno es una generalización del teorema de Pitágoras en los triángulos. El teorema relaciona un lado de un triángulo cualquiera con los otros dos y con el coseno del ángulo formado por estos dos lados.

$$ \Large \textcolor{blue}{ \fbox{ $ \array{ \cr \quad \mathbf{ a^2 = b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos \hat{A} } \quad \cr \quad \mathbf{ b^2 = a^2 + c^2 - 2 \cdot a \cdot c \cdot \cos \hat{B} } \quad \cr \quad \mathbf{ c^2 = a^2 + b^2 - 2 \cdot a \cdot b \cdot \cos \hat{C} } \quad \cr \quad } $ } } $$

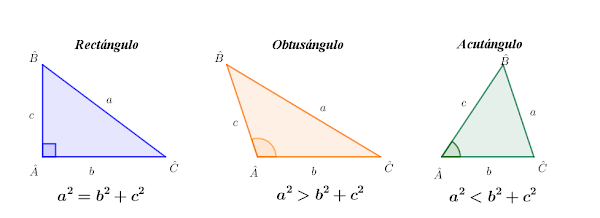
Veamos como podemos saber el tipo de triángulo según sus ángulos usando el Teorema del coseno:

• Si tiene una ángulo recto $\hat{A} = \dfrac{\ \pi \ }{2} \Rightarrow \cos \hat{A} = 0 $, triángulo rectángulo se cumple:
  $$ \mathbf{ a^2 = b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos \hat{A} \Rightarrow a^2 = b^2 + c^2 \qquad \text{ (Teorema de Pitágoras)} } $$
  
• Si tiene una ángulo obtuso $\hat{A} > \dfrac{\ \pi \ }{2} \Rightarrow \cos \hat{A} < 0 $, triángulo obtusángulo se cumple:
  $$ \mathbf{ a^2 = b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos \hat{A} \Rightarrow a^2 > b^2 + c^2 } $$
  
• Si tiene una ángulo agudo $\hat{A} < \dfrac{\ \pi \ }{2} \Rightarrow \cos \hat{A} > 0 $, triángulo acutángulo se cumple:
  $$ \mathbf{ a^2 = b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos \hat{A} \Rightarrow a^2 < b^2 + c^2 } $$
  

Ocurre lo mismo si cogemos el ángulo $\hat{B}$ o el ángulo $\hat{C}$.

Teorema del coseno (Usando el Producto Escalar) 

El teorma del coseno se puede demostrar también usando el producto escalar. Del dibujo tenemos:

$$ \overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC} \Leftrightarrow  \overrightarrow{BC} = \overrightarrow{AC} - \overrightarrow{AB} $$ 

$$ \overrightarrow{BC} \cdot \overrightarrow{BC} = \left ( \overrightarrow{AC} - \overrightarrow{AB} \right ) \cdot \left ( \overrightarrow{AC} - \overrightarrow{AB} \right ) = \overrightarrow{AC} \cdot \overrightarrow{AC} + \overrightarrow{AB} \cdot \overrightarrow{AB} - 2 \cdot \overrightarrow{AC} \cdot \overrightarrow{AB} $$

Recapitulando:

$$ |\overrightarrow{BC}|^2 = |\overrightarrow{AC}|^2 + |\overrightarrow{AB}|^2 - 2 |\overrightarrow{AC}| \cdot |\overrightarrow{AB}| \cdot \cos \hat{A}$$

Es decir

$$ a^2 = b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos \hat{A} $$

Ventajas e incovenientes de usar el teorema del seno o del coseno

	Teorema del seno	Teorema del coseno
Ventajas	Fácil de calcular	El coseno de un ángulo tiene un único valor entre 0 y $\pi$ radianes.
Incovenientes	El seno de un ángulo y su suplementario tienen el mismo valor. Dos posibles soluciones.	No es tan fácil de calcular como el Teorema del seno.

Teorema de la tangente es una fórmula que relaciona las longitudes de los tres lados de un triángulo y las tangentes de sus ángulos.

Para demostrar el teorema de la tangente tenemos que hacer uno de una propiedad de las proporciones:

$$ \dfrac{x}{y} = \dfrac{z}{t} \ \ \Longleftrightarrow \ \ x \cdot t = y \cdot z \ \ \ \  \text{entonces}  \ \ \Longrightarrow  \dfrac{x + y}{x - y} = \dfrac{z + t}{z - t}  $$

$$ \text{Tenemos } \ \  \dfrac{a}{\sen \hat{A}} = \dfrac{b}{\sen \hat{B}}  \ \ \Longleftrightarrow \ \ \dfrac{a}{b} = \dfrac{\sen \hat{A}}{\sen \hat{B}} $$ 

Aplicando esta propiedad al teorema del seno: 

$$ \dfrac{ a + b}{a - b} = \dfrac{\sen \hat{A} + \sen \hat{B}}{\sen \hat{A} - \sen \hat{B}} = \dfrac{2 \cdot \sen \left ( \dfrac{\hat{A} + \hat{B}}{2} \right ) \cdot \cos \left ( \dfrac{\hat{A} - \hat{B}}{2} \right ) }{2 \cdot \cos \left ( \dfrac{\hat{A} + \hat{B}}{2} \right ) \cdot \sen \left ( \dfrac{\hat{A} - \hat{B}}{2} \right ) } = \dfrac{ \tg \left ( \dfrac{\hat{A} + \hat{B}}{2} \right ) }{ \tg \left ( \dfrac{\hat{A} - \hat{B}}{2} \right ) } $$

$$ \Large \textcolor{blue}{ \fbox{ $ \array{ \cr \quad \mathbf{ \dfrac{ a + b}{a - b} = \dfrac{ \tg \left ( \dfrac{\hat{A} + \hat{B}}{2} \right ) }{ \tg \left ( \dfrac{\hat{A} - \hat{B}}{2} \right ) } = 2R} \quad \cr \quad \cr \mathbf{ \dfrac{ a + c}{a - c} = \dfrac{ \tg \left ( \dfrac{\hat{A} + \hat{C}}{2} \right ) }{ \tg \left ( \dfrac{\hat{A} - \hat{C}}{2} \right ) } = 2R} \quad \cr \quad \cr \mathbf{ \dfrac{ b + c}{b - c} = \dfrac{ \tg \left ( \dfrac{\hat{B} + \hat{C}}{2} \right ) }{ \tg \left ( \dfrac{\hat{B} - \hat{C}}{2} \right ) } = 2R} \cr \quad } $ } } $$

Entrada del blog donde se explican la interpretación geométrica de las razones trigonométricas de un ángulo del primer cuadrante, y el seno, coseno de la suma de ángulos.

Entrada del blog donde se indican las razones trigonométricas de los ángulos notables entre $[0, 2\pi]$ y las conversiones de grados a radianes, de radianes a grados, de grados decimales a sexagesimales y de grados sexagesimales a decimales.

Vamos con algunos ejercicios de resolución de triángulos no rectángulos

Cosas a tener en cuenta:

1. La suma de los ángulos internos de un triángulo suma $\gss{180} = \widehat{A} + \widehat{B} + \widehat{C}$.
   
   
2. Las longitudes de los Lados del Triángulo deben cumplir la condición de existencia del triángulo que establece, que la suma de las longitudes de dos lados cualesquiera siempre debe ser mayor que la longitud del tercer lado. Este es un pilar fundamental en la definición de un triángulo.
   
   $$ \cases{ a + b > c \cr \cr a + c > b \cr \cr b + c > a \cr } $$
3. El lado más largo se encuentra frente al ángulo más grande y el lado más pequeño frente al ángulo más pequeño.
   
   

Queremos calcular el lado $c$, para ello usaremos el Teorema del Coseno: $$ c^2 = a^2 + b^2 - 2bc \cos \widehat{C} $$ Sustituyendo las variables por su valor, que $\cos \gss{120} = \dfrac{\ -1\ }{ 2 } $ tenemos que:
$$ c^2 = 5^2 + 3^2 - 2\cdot 5 \cdot 3 \cdot \cos \gss{120} \Rightarrow c^2 = 25 + 9 - 2 \cdot 5 \cdot 3 \cdot \left ( \dfrac{\ -1\ }{ 2 } \right) \Rightarrow $$ $$ \Rightarrow c^2 = 25 + 9 + 15 \Rightarrow c^2 = 49 \Rightarrow c= 7 $$ Ahora calculamos cualquiera de los ángulos que nos quedan $\widehat{A} $ o $\widehat{B}$, vamos con $\widehat{B}$: $$ b^2 = a^2 + c^2 - 2ac \cos \widehat{B} \Rightarrow 2ac \cos \widehat{B} = a^2 + c^2 - b^2 \Rightarrow \cos \widehat{B} = \dfrac{\ a^2 + c^2 - b^2\ }{ 2ac } $$ Sustituyendo los datos en las variables: $$ \cos \widehat{B} = \dfrac{\ a^2 + c^2 - b^2\ }{ 2ac } = \dfrac{\ 5^2 + 7^2 - 3^2\ }{ 2 \cdot 5 \cdot 7 } = \dfrac{\ 65\ }{ 70 } = \dfrac{\ 13\ }{ 14 } $$ Es decir: $$ \widehat{B} = \arccos \left ( \dfrac{\ 13\ }{ 14 } \right) = \gss{21,79} = \gss{21} 47' 24''$$ Y por tanto $$ \widehat{A} = \gss{38,21} = \gss{38} 12' 36'' $$